题目内容
【题目】已知在极坐标系中曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,以极点为坐标原点,以极轴为
,以极点为坐标原点,以极轴为![]() 轴的正半轴建立直角坐标系,曲线
轴的正半轴建立直角坐标系,曲线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),点
为参数),点![]() .
.
(1)求出曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线
,曲线![]() :
:![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)根据![]() ,
,![]() 将曲线
将曲线![]() 的极坐标方程化为直角坐标方程,根据加减消元法得曲线
的极坐标方程化为直角坐标方程,根据加减消元法得曲线![]() 的普通方程;(2)将直线参数方程代入曲线
的普通方程;(2)将直线参数方程代入曲线![]() 的直角坐标方程,结合韦达定理即可求得
的直角坐标方程,结合韦达定理即可求得![]() 的值.
的值.
试题解析:(1)∵![]() ,当
,当![]() 时,有
时,有![]()
∴![]()
当![]() 时,点
时,点![]() 在曲线
在曲线![]() 上,
上,![]() 即是在直角坐标系中的原点(0,0)满足方程
即是在直角坐标系中的原点(0,0)满足方程![]() .
.
故曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 即
即![]() .
.
曲线![]() :
:![]() .
.
(2)将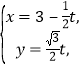 代入
代入![]() 得
得![]() ,
,
![]() ,故方程有两个不等实根
,故方程有两个不等实根![]() 分别对应点
分别对应点![]() .
.
∴![]() ,即
,即![]() =
=![]() .
.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目