【题目】如图，已知正方体的棱长为2，则以下四个命题中错误的是

A. 直线与为异面直线 B. 平面

C. D. 三棱锥的体积为

【题目】在直角坐标系xOy中，直线l1的参数方程为 ，（t为参数），直线l2的参数方程为 ，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．
（Ⅰ）写出C的普通方程；
（Ⅱ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣ =0，M为l3与C的交点，求M的极径．

【题目】某单位员工人参加“学雷锋”志愿活动，按年龄分组：第组，第组,第组,第组,第组，得到的频率分布直方图如图所示.

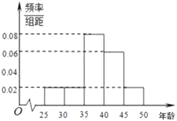
（1）下表是年龄的频率分布表，求正整数的值；

（2）现在要从年龄较小的第组中用分层抽样的方法抽取人，年龄在第组抽取的员工的人数分别是多少？

（3）在（2）的前提下，从这人中随机抽取人参加社区宣传交流活动，求至少有人年龄在第组的概率.

【题目】已知函数f（x）=x﹣1﹣alnx．
（Ⅰ）若 f（x）≥0，求a的值；
（Ⅱ）设m为整数，且对于任意正整数n，（1+ ）（1+ ）…（1+ ）＜m，求m的最小值．

【题目】已知抛物线C：y2=2x，过点（2，0）的直线l交C与A，B两点，圆M是以线段AB为直径的圆．
（Ⅰ）证明：坐标原点O在圆M上；
（Ⅱ）设圆M过点P（4，﹣2），求直线l与圆M的方程．

(1)画出散点图．观察散点图，说明两个变量有怎样的相关关系；

(2)用最小二乘法计算利润额关于销售额的回归直线方程；

(3)当销售额为4千万元时，利用(2)的结论估计该零售店的利润额(百万元)．

[参考公式：，]

【题目】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．
（Ⅰ）证明：平面ACD⊥平面ABC；
（Ⅱ）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．

以最高气温位于各区间的频率代替最高气温位于该区间的概率．
（Ⅰ）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；
（Ⅱ）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？

【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知sinA+ cosA=0，a=2 ，b=2．
（Ⅰ）求c；
（Ⅱ）设D为BC边上一点，且AD⊥AC，求△ABD的面积．