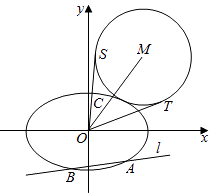题目内容
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程.
【答案】解:方法一:证明:(Ⅰ)当直线l的斜率不存在时,则A(2,2),B(2,﹣2),
则 ![]() =(2,2),
=(2,2), ![]() =(2,﹣2),则
=(2,﹣2),则 ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
则坐标原点O在圆M上;
当直线l的斜率存在,设直线l的方程y=k(x﹣2),设A(x1 , y1),B(x2 , y2),![]() ,整理得:k2x2﹣(4k2+2)x+4k2=0,
,整理得:k2x2﹣(4k2+2)x+4k2=0,
则x1x2=4,4x1x2=y12y22=(y1y2)2 , 由y1y2<0,
则y1y2=﹣4,
由 ![]()
![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
则 ![]() ⊥
⊥ ![]() ,则坐标原点O在圆M上,
,则坐标原点O在圆M上,
综上可知:坐标原点O在圆M上;
方法二:设直线l的方程x=my+2,![]() ,整理得:y2﹣2my﹣4=0,设A(x1 , y1),B(x2 , y2),
,整理得:y2﹣2my﹣4=0,设A(x1 , y1),B(x2 , y2),
则y1y2=﹣4,
则(y1y2)2=4x1x2 , 则x1x2=4,则 ![]()
![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
则 ![]() ⊥
⊥ ![]() ,则坐标原点O在圆M上,
,则坐标原点O在圆M上,
∴坐标原点O在圆M上;
(Ⅱ)由(Ⅰ)可知:x1x2=4,x1+x2= ![]() ,y1+y2=
,y1+y2= ![]() ,y1y2=﹣4,
,y1y2=﹣4,
圆M过点P(4,﹣2),则 ![]() =(4﹣x1 , ﹣2﹣y1),
=(4﹣x1 , ﹣2﹣y1), ![]() =(4﹣x2/span> , ﹣2﹣y2),
=(4﹣x2/span> , ﹣2﹣y2),
由 ![]()
![]() =0,则(4﹣x1)(4﹣x2)+(﹣2﹣y1)(﹣2﹣y2)=0,
=0,则(4﹣x1)(4﹣x2)+(﹣2﹣y1)(﹣2﹣y2)=0,
整理得:k2+k﹣2=0,解得:k=﹣2,k=1,
当k=﹣2时,直线l的方程为y=﹣2x+4,
则x1+x2= ![]() ,y1+y2=﹣1,
,y1+y2=﹣1,
则M( ![]() ,﹣
,﹣ ![]() ),半径为r=丨MP丨=
),半径为r=丨MP丨= ![]() =
= ![]() ,
,
∴圆M的方程(x﹣ ![]() )2+(y+
)2+(y+ ![]() )2=
)2= ![]() .
.
当直线斜率k=1时,直线l的方程为y=x﹣2,
同理求得M(3,1),则半径为r=丨MP丨= ![]() ,
,
∴圆M的方程为(x﹣3)2+(y﹣1)2=10,
综上可知:直线l的方程为y=﹣2x+4,圆M的方程(x﹣ ![]() )2+(y+
)2+(y+ ![]() )2=
)2= ![]()
或直线l的方程为y=x﹣2,圆M的方程为(x﹣3)2+(y﹣1)2=10.
【解析】(Ⅰ)方法一:分类讨论,当直线斜率不存在时,求得A和B的坐标,由 ![]()
![]() =0,则坐标原点O在圆M上;当直线l斜率存在,代入抛物线方程,利用韦达定理及向量数量积的可得
=0,则坐标原点O在圆M上;当直线l斜率存在,代入抛物线方程,利用韦达定理及向量数量积的可得 ![]()
![]() =0,则坐标原点O在圆M上;
=0,则坐标原点O在圆M上;
方法二:设直线l的方程x=my+2,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得 ![]()
![]() =0,则坐标原点O在圆M上;
=0,则坐标原点O在圆M上;
(Ⅱ)由题意可知: ![]()
![]() =0,根据向量数量积的坐标运算,即可求得k的值,求得M点坐标,则半径r=丨MP丨,即可求得圆的方程.
=0,根据向量数量积的坐标运算,即可求得k的值,求得M点坐标,则半径r=丨MP丨,即可求得圆的方程.
【考点精析】本题主要考查了点斜式方程和斜截式方程的相关知识点,需要掌握直线的点斜式方程:直线![]() 经过点
经过点![]() ,且斜率为
,且斜率为![]() 则:
则:![]() ;直线的斜截式方程:已知直线
;直线的斜截式方程:已知直线![]() 的斜率为
的斜率为![]() ,且与
,且与![]() 轴的交点为
轴的交点为![]() 则:
则:![]() 才能正确解答此题.
才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某县教育局为了检查本县甲、乙两所学校的学生对安全知识的学习情况,在这两所学校进行了安全知识测试,随机在这两所学校各抽取20名学生的考试成绩作为样本,成绩大于或等于80分的为优秀,否则为不优秀,统计结果如下图:


甲校 乙校
(1)从乙校成绩优秀的学生中任选两名,求这两名学生的成绩恰有一个落在![]() 内的概率;
内的概率;
(2)由以上数据完成下面列联表,并回答能否在犯错的概率不超过0.1的前提下认为学生的成绩与两所学校的选择有关。
甲校 | 乙校 | 总计 | |
优秀 | |||
不优秀 | |||
总计 |
![]()
参考数据 | P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |