【题目】平潭国际“花式风筝冲浪”集训队，在平潭龙凤头海滨浴场进行集训，海滨区域的某个观测点观测到该处水深（米）是随着一天的时间呈周期性变化，某天各时刻的水深数据的近似值如下表：

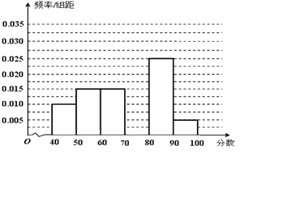
（Ⅰ）根据表中近似数据画出散点图（坐标系在答题卷中）.观察散点图，从

①， ②，③

中选择一个合适的函数模型，并求出该拟合模型的函数解析式；（Ⅱ）为保证队员安全，规定在一天中的5～18时且水深不低于1.05米的时候进行训练，根据（Ⅰ） 中的选择的函数解析式，试问：这一天可以安排什么时间段组织训练，才能确保集训队员的安全。

【题目】某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用表示该学生选修的课程门数和没有选修的课程门数的乘积．

（1）记“函数为上的偶函数”为事件，求事件的概率；

（2）求的分布列和数学期望．

【题目】已知为坐标原点，对于函数，称向量为函数的伴随向量，同时称函数为向量的伴随函数．

（Ⅰ）设函数，试求的伴随向量；

（Ⅱ）记向量的伴随函数为，求当且时的值；

（Ⅲ）由（Ⅰ）中函数的图像（纵坐标不变）横坐标伸长为原来的倍，再把整个图像向右平移个单位长度得到的图像。已知 ，问在的图像上是否存在一点，使得.若存在，求出点坐标；若不存在，说明理由。

【题目】设函数,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.

(1)求 (2)证明:

(1)甲从其中一个箱子中摸出一个球，乙从另一个箱子摸出一个球，谁摸出的球上标的数字大谁就获胜（若数字相同则为平局），求甲获胜的概率；

(2)摸球方法与（1）同，若规定：两人摸到的球上所标数字相同甲获胜，所标数字不相同则乙获胜，这样规定公平吗？请说明理由。

【题目】在直角坐标系中，已知曲线（为参数），在以为极点， 轴正半轴为极轴的极坐标系中，曲线，曲线.

（1）求曲线与的交点的直角坐标；

（2）设点， 分别为曲线上的动点，求的最小值.

【题目】在如图所示的三棱锥中，分别是的中点．

（1）求证：平面；

（2）若为正三角形，且为上的一点，，求直线与直线所成角的正切值．

（Ⅰ）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；

(Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分；

(Ⅲ) 从成绩在[40，50）和[90，100]的学生中任选两人，求他们在同一分数段的概率.

【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，作了初步处理，得到下表：

（1）从3月1日至3月5日中任选2天，记发芽的种子数分别为，求事件“均小于26”的概率；

（2）请根据3月1日至3月5日的数据，求出关于的线性回归方程，并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽（取整数值）．

附：回归方程中的斜率和截距最小二乘法估计公式分别为：，，，．

【题目】在如图所示的三棱锥中，底面分别是的中点．

（1）求证：平面；

（2）若，求直线与平面所成角的正切值．