15．在100个零件中，有一级品20个，二级品30个，三级品50个，从中抽取20个作为样本：①采用随机抽样法，将零件编号为00，01，02，…，99，抽出20个；②采用系统抽样法，将所有零件分成20组，每组5个，然后每组中随机抽取1个；③采用分层抽样法，随机从一级品中抽取4个，二级品中抽取6个，三级品中抽取10个；则（ ）
| A． | 不论采取哪种抽样方法，这100个零件中每个被抽到的概率都是$\frac{1}{5}$ | |
| B． | ①②两种抽样方法，这100个零件中每个被抽到的概率都是$\frac{1}{5}$，③并非如此 | |
| C． | ①③两种抽样方法，这100个零件中每个被抽到的概率都是$\frac{1}{5}$，②并非如此 | |
| D． | 采用不同的抽样方法，这100个零件中每个被抽到的概率各不相同 |
8．设不等式$\left\{\begin{array}{l}{x+y≤4}\\{y-x≥0}\\{x-1≥0}\end{array}\right.$表示的平面区域为D，若圆C：（x+1）2+（y+1）2=r2（r＞0）经过区域D上的点，则r的取值范围是（ ）
0 250583 250591 250597 250601 250607 250609 250613 250619 250621 250627 250633 250637 250639 250643 250649 250651 250657 250661 250663 250667 250669 250673 250675 250677 250678 250679 250681 250682 250683 250685 250687 250691 250693 250697 250699 250703 250709 250711 250717 250721 250723 250727 250733 250739 250741 250747 250751 250753 250759 250763 250769 250777 266669
| A． | （-∞，2$\sqrt{2}$）∪（2$\sqrt{5}$，+∞） | B． | （2$\sqrt{2}$，3$\sqrt{2}$] | C． | （3$\sqrt{2}$，2$\sqrt{5}$] | D． | [2$\sqrt{2}$，2$\sqrt{5}$] |
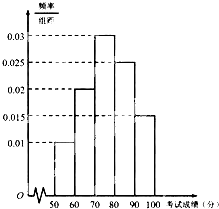某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．