5.三棱锥P-ABC的四个顶点都在球O的表面上,PA⊥平面ABC,AB⊥BC,PA=2,AB=BC=1,则球O的表面积为( )
| A. | $\sqrt{6}$π | B. | 6π | C. | 24π | D. | 2$\sqrt{6}$π |
3.已知等差数列{an}的前n项和为Sn,公差为1,若S6=3S3,则a9=( )
| A. | 11 | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
2.在△ABC中,D点为边BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
| A. | 2($\overrightarrow{a}$+$\overrightarrow{b}$) | B. | 2($\overrightarrow{a}$-$\overrightarrow{b}$) | C. | $\frac{1}{2}$($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) |
1.已知数列{an}满足a1=1,且对任意的正整数n,有an+1=2an成立,则a3a5=( )
| A. | $\frac{1}{64}$ | B. | 32 | C. | 64 | D. | $\frac{1}{32}$ |
20.下列说法正确的是( )
| A. | 命题“若x=1,则x2=1”的否命题是“x=1,则x2≠1” | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | “(x-1)(x+3)<0”是“-2<x<1”的充分不必要条件 | |
| D. | 若p∨q为假命题,则p,q中至少有一个是假命题 |
19.已知i为虚数单位,复数z=$\frac{1-i}{2+i}$,则z的共轭复数是( )
| A. | $\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{3}$-i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | $\frac{1}{3}$+i |
18.设集合U={1,2,3,4,5,6,7},集合A={1,2,5,7},则∁UA=( )
0 241181 241189 241195 241199 241205 241207 241211 241217 241219 241225 241231 241235 241237 241241 241247 241249 241255 241259 241261 241265 241267 241271 241273 241275 241276 241277 241279 241280 241281 241283 241285 241289 241291 241295 241297 241301 241307 241309 241315 241319 241321 241325 241331 241337 241339 241345 241349 241351 241357 241361 241367 241375 266669
| A. | {1,2,5,7} | B. | {3,4,6} | C. | {6} | D. | U |
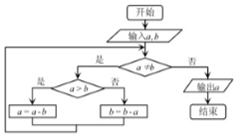 如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为8,18,则输出的a等于( )
如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为8,18,则输出的a等于( )