题目内容
19．已知i为虚数单位，复数z=$\frac{1-i}{2+i}$，则z的共轭复数是（ ）| A． | $\frac{1}{5}$+$\frac{3}{5}$i | B． | $\frac{1}{3}$-i | C． | $\frac{1}{5}$-$\frac{3}{5}$i | D． | $\frac{1}{3}$+i |
分析 利用复数代数形式的乘除运算化简z，再由共轭复数的概念得答案．
解答 解：∵z=$\frac{1-i}{2+i}$=$\frac{（1-i）（2-i）}{（2+i）（2-i）}=\frac{1-3i}{5}=\frac{1}{5}-\frac{3}{5}i$，
∴$\overline{z}=\frac{1}{5}+\frac{3}{5}i$．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4．若集合A={0，1，2}，B={x|x2≤4，x∈N}，则A∩B=（ ）
| A． | {x|0≤x≤2} | B． | {x|-2≤x≤2} | C． | {0，1，2} | D． | {1，2} |
10．在空间直角坐标系O-xyz中，已知A（1，2，-1），B（1，2，1），则|AB|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{5}$ | D． | 2$\sqrt{5}$ |
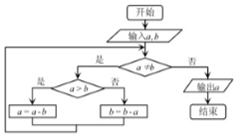如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b分别为8，18，则输出的a等于（ ）