18．已知点P为棱长等于2的正方体ABCD-A1B1C1D1内部一动点.且$|{\overrightarrow{PA}}|=2$.则$\overrightarrow{P{C 1}}•\ov——青夏教育精英家教网——

18．已知点P为棱长等于2的正方体ABCD-A₁B₁C₁D₁内部一动点，且$|{\overrightarrow{PA}}|=2$，则$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值达到最小时，$\overrightarrow{P{C_1}}$与$\overrightarrow{P{D_1}}$夹角大小为90°．

如图，三角形ABC中，AB=1，$BC=\sqrt{3}$，以C为直角顶点向外作等腰直角三角形ACD，当∠ABC变化时，线段BD的长度最大值为（　　）

16．各项均为正数的等差数列{a_n}中，前n项和为S_n，当n∈N^*，n≥2时，有${S_n}=\frac{n}{n-1}（{a_n}^2-{a_1}^2）$，则S₂₀-2S₁₀=（　　）

15．已知a，b，c分别为△ABC的三个内角A，B，C的对边，若a²-c²=2b，sinB=4cosA•sinC，则b=（　　）

14．设A（0，1），B（1，3），C（-1，5），D（0，-1），则$\overrightarrow{AB}+\overrightarrow{AC}$等于（　　）

-2$\overrightarrow{AD}$

2$\overrightarrow{AD}$

-3$\overrightarrow{AD}$

3$\overrightarrow{AD}$

13．已知圆M：（x-a）²+（y-b）²=9，M在抛物线C：x²=2py（p＞0）上，圆M过原点且与C的准线相切．
（Ⅰ）求C的方程；
（Ⅱ）点Q（0，-t）（t＞0），点P（与Q不重合）在直线l：y=-t上运动，过点P作C的两条切线，切点分别为A，B．求证：∠AQO=∠BQO（其中O为坐标原点）．

12．某工厂的污水处理程序如下：原始污水必先经过A系统处理，处理后的污水（A级水）达到环保标准（简称达标）的概率为p（0＜p＜1）．经化验检测，若确认达标便可直接排放；若不达标则必须进行B系统处理后直接排放．
某厂现有4个标准水量的A级水池，分别取样、检测．多个污水样本检测时，既可以逐个化验，也可以将若干个样本混合在一起化验．混合样本中只要有样本不达标，则混合样本的化验结果必不达标．若混合样本不达标，则该组中各个样本必须再逐个化验；若混合样本达标，则原水池的污水直接排放．
现有以下四种方案，
方案一：逐个化验；
方案二：平均分成两组化验；
方案三：三个样本混在一起化验，剩下的一个单独化验；
方案四：混在一起化验．
化验次数的期望值越小，则方案的越“优”．
（Ⅰ）若$p=\frac{2}{{\sqrt{5}}}$，求2个A级水样本混合化验结果不达标的概率；
（Ⅱ）若$p=\frac{2}{{\sqrt{5}}}$，现有4个A级水样本需要化验，请问：方案一，二，四中哪个最“优”？
（Ⅲ）若“方案三”比“方案四”更“优”，求p的取值范围．

11．在数列{a_n}中，a₁=1，a_n+1=（n+1）a_n+（n+1）!．
（Ⅰ）求证：数列$\left\{{\frac{a_n}{n!}}\right\}$是等差数列，并求{a_n}的通项公式；
（Ⅱ）求{a_n}的前n项和S_n．

10．5支篮球队进行单循环比赛（任两支球队恰进行一场比赛），任两支球队之间胜率都是$\frac{1}{2}$．单循环比赛结束，以获胜的场次数作为该队的成绩，成绩按从大到小排名次顺序，成绩相同则名次相同．有下列四个命题：p₁：恰有四支球队并列第一名为不可能事件；p₂：有可能出现恰有两支球队并列第一名；p₃：每支球队都既有胜又有败的概率为$\frac{17}{32}$；p₄：五支球队成绩并列第一名的概率为$\frac{3}{32}$．其中真命题是（　　）

p₁，p₂，p₃

p₁，p₂，p₄

p₁，p₃，p₄

p₂，p₃，p₄

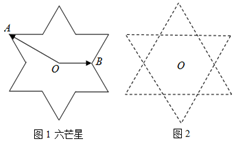如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（　　）

$[{-\sqrt{21}，\sqrt{21}}]$

0 239722 239730 239736 239740 239746 239748 239752 239758 239760 239766 239772 239776 239778 239782 239788 239790 239796 239800 239802 239806 239808 239812 239814 239816 239817 239818 239820 239821 239822 239824 239826 239830 239832 239836 239838 239842 239848 239850 239856 239860 239862 239866 239872 239878 239880 239886 239890 239892 239898 239902 239908 239916 266669