17.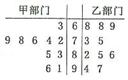 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
(1)若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号,求从这20名员工中任选三人,其中恰有两人获得“职业技能好能手”的概率;
(2)公司结合这次测试成绩对员工的绩效奖金进行调整(绩效奖金方案如表),若以甲部门这10人的样本数据来估计该部门总体数据,且以频率估计概率,从甲部门所有员工中任选3名员工,记绩效奖金不小于3a的人数为ξ,求ξ的分布列及数学期望.
 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.(1)若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号,求从这20名员工中任选三人,其中恰有两人获得“职业技能好能手”的概率;
(2)公司结合这次测试成绩对员工的绩效奖金进行调整(绩效奖金方案如表),若以甲部门这10人的样本数据来估计该部门总体数据,且以频率估计概率,从甲部门所有员工中任选3名员工,记绩效奖金不小于3a的人数为ξ,求ξ的分布列及数学期望.
| 分数 | [60,70) | [70,80) | [80,90) | [90,100] |
| 奖金 | a | 2a | 3a | 4a |
16.设A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点,F(c,0)是右焦点,若抛物线${y^2}=-\frac{{4{a^2}}}{c}x$的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
15.函数f(x)=(1-cos2x)cos2x,x∈R,设f(x)的最大值是A,最小正周期为T,则f(AT)的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
14.等差数列{an}满足a1=1,a2+a3=3,则a1+a2+a3+a4+a5+a6+a7=( )
| A. | 7 | B. | 14 | C. | 21 | D. | 28 |
13.已知集合A={x|x2+x-6<0},B={-2,-1,0,1,2},那么A∩B=( )
0 239646 239654 239660 239664 239670 239672 239676 239682 239684 239690 239696 239700 239702 239706 239712 239714 239720 239724 239726 239730 239732 239736 239738 239740 239741 239742 239744 239745 239746 239748 239750 239754 239756 239760 239762 239766 239772 239774 239780 239784 239786 239790 239796 239802 239804 239810 239814 239816 239822 239826 239832 239840 266669
| A. | {-2,-1,0,1} | B. | {-2,-1,1} | C. | {-1,1,2} | D. | {-1,0,1,2} |
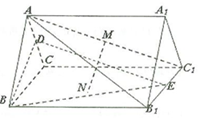 如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.
如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.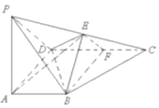 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点