15.为了监控某种零件的一条生产线的生产过程,检验员每隔30min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
经计算得 $\overline{x}$=$\frac{1}{16}$$\sum_{i=1}^{16}$xi=9.97,s=$\sqrt{\frac{1}{16}\sum_{i=1}^{16}({x}_{i}-\overline{x})^{2}}$=$\sqrt{\frac{1}{16}(\sum_{i=1}^{16}{{x}_{i}}^{2}-16{\overline{x}}^{2})$≈0.212,$\sqrt{\sum_{i=1}^{16}(i-8.5)^{2}}$≈18.439,$\sum_{i=1}^{16}$(xi-$\overline{x}$)(i-8.5)=-2.78,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在($\overline{x}$-3s,$\overline{x}$+3s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在($\overline{x}$-3s,$\overline{x}$+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}\sqrt{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,$\sqrt{0.008}$≈0.09.
| 抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在($\overline{x}$-3s,$\overline{x}$+3s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在($\overline{x}$-3s,$\overline{x}$+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}\sqrt{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,$\sqrt{0.008}$≈0.09.
12.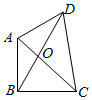 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
0 239620 239628 239634 239638 239644 239646 239650 239656 239658 239664 239670 239674 239676 239680 239686 239688 239694 239698 239700 239704 239706 239710 239712 239714 239715 239716 239718 239719 239720 239722 239724 239728 239730 239734 239736 239740 239746 239748 239754 239758 239760 239764 239770 239776 239778 239784 239788 239790 239796 239800 239806 239814 266669
 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
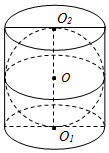 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.
如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.