15.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则cos(2α-β)的取值范围为( )
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
14.函数$y={log_{\frac{1}{3}}}({-{x^2}+2x+3})$的单调增区间是( )
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
12.设复数z满足z2=3-4i,则z的模是( )
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{3}$ | D. | 1 |
7. 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
由表中的数据显示,x与y之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出y关于x的回归直线方程.
0 239009 239017 239023 239027 239033 239035 239039 239045 239047 239053 239059 239063 239065 239069 239075 239077 239083 239087 239089 239093 239095 239099 239101 239103 239104 239105 239107 239108 239109 239111 239113 239117 239119 239123 239125 239129 239135 239137 239143 239147 239149 239153 239159 239165 239167 239173 239177 239179 239185 239189 239195 239203 266669
 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
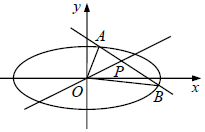 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.