18．已知函数$f(x)=lnx-\frac{{m}}{x+1}$上不单调.若m-n＞λ恒成立.则实数λ的取值范围为( )A．[3.+∞)B．[4.+∞)C．(-∞.3]D．(-∞.4]——青夏教育精英家教网——

18．已知函数$f（x）=lnx-\frac{{m（{x+n}）}}{x+1}$（m＞0，n∈R）在（0，+∞）上不单调，若m-n＞λ恒成立，则实数λ的取值范围为（　　）

17．实数m取什么数值时，复数z=（m-4）+（m²-5m-6）i分别是：
（Ⅰ）实数？
（Ⅱ）虚数？
（Ⅲ）纯虚数？

16．若复数z满足i（z+1）=-3+2i，则z的虚部是3．

15．已知$\frac{a+2i}{i}$=b+i（其中a，b∈R，i为虚数单位），则a+b的值为（　　）

14．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，左焦点是F₁．
（1）若左焦点F₁与椭圆E的短轴的两个端点是正三角形的三个顶点，点$Q（{\sqrt{3}，\frac{1}{2}}）$在椭圆E上．求椭圆E的方程；
（2）过原点且斜率为t（t＞0）的直线l₁与（1）中的椭圆E交于不同的两点G，H，设B₁（0，1），A₁（2，0），求四边形A₁GB₁H的面积取得最大值时直线l₁的方程；
（3）过左焦点F₁的直线l₂交椭圆E于M，N两点，直线l₂交直线x=-p（p＞0）于点P，其中p是常数，设$\overrightarrow{PM}=λ\overrightarrow{M{F_1}}$，$\overrightarrow{PN}=μ\overrightarrow{N{F_1}}$，计算λ+μ的值（用p，a，b的代数式表示）．

13．已知数列{a_n}的前n项和为S_n，且S_n=2a_n-2（n∈N^*）．
（1）求{a_n}的通项公式；
（2）设${b_{n+1}}=2{b_n}-{2^{n+1}}$，b₁=8，T_n是数列{b_n}的前n项和，求正整数k，使得对任意n∈N^*均有T_k≥T_n恒成立；
（3）设${c_n}=\frac{{{a_{\;n\;+\;1}}}}{{（1+{a_n}）（1+{a_{\;n\;+\;1}}）}}$，R_n是数列{c_n}的前n项和，若对任意n∈N^*均有R_n＜λ恒成立，求λ的最小值．

12．下列说法正确的是（　　）

	A．	存在x₀∈R，使得$1-{cos^3}{x_0}={log_2}\frac{1}{10}$
	B．	函数y=sin2xcos2x的最小正周期为π
	C．	函数$y=cos2（{x+\frac{π}{3}}）$的一个对称中心为$（{-\frac{π}{3}，0}）$
	D．	角α的终边经过点（cos（-3），sin（-3）），则角α是第三象限角

11．点M（x，y）在圆x²+（y-2）²=1上运动，则$\frac{xy}{{4{x^2}+{y^2}}}$的取值范围是（　　）

（-∞，-$\frac{1}{4}$]∪[$\frac{1}{4}$，+∞）

（-∞，-$\frac{1}{4}$]∪[$\frac{1}{4}$，+∞）∪{0}

$[{-\frac{1}{4}，0}）∪（{0，\frac{1}{4}}]$

$[{-\frac{1}{4}，\frac{1}{4}}]$

10．由3个1和3个0组成的二进制的数有20个．

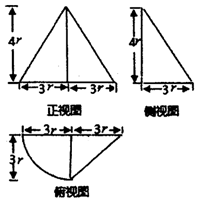已知一个简单几何的三视图如图所示，若该几何体的体积为24π+48，则该几何体的表面积为（　　）

$24π+90+6\sqrt{41}$

$24π+66+6\sqrt{41}$

0 238954 238962 238968 238972 238978 238980 238984 238990 238992 238998 239004 239008 239010 239014 239020 239022 239028 239032 239034 239038 239040 239044 239046 239048 239049 239050 239052 239053 239054 239056 239058 239062 239064 239068 239070 239074 239080 239082 239088 239092 239094 239098 239104 239110 239112 239118 239122 239124 239130 239134 239140 239148 266669