18.若y=f(x)是定义域在R上的函数,则y=f(x)为奇函数的一个充要条件为( )
| A. | f(0)=0 | B. | 对?x∈R,f(x)=0都成立 | ||
| C. | ?x0∈R,使得f(x0)+f(-x0)=0 | D. | 对?x∈R,f(x)+f(-x)=0都成立 |
17.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}+1}{2}$ | D. | $\sqrt{2}$+1 |
16.已知定义在R上的偶函数f(x),满足f(x+4)=f(x),且x∈[0,2]时,f(x)=sinπx+2|sinπx|,则方程f(x)-|lgx|=0在区间[0,10]上根的个数是( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
14.若数列{an}是正项数列,且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=n2+n,则a1+$\frac{{a}_{2}}{2}$+…+$\frac{{a}_{n}}{n}$等于( )
| A. | 2n2+2n | B. | n2+2n | C. | 2n2+n | D. | 2(n2+2n) |
13.已知某几何体的三视图如图所示,则该几何体的体积是( )
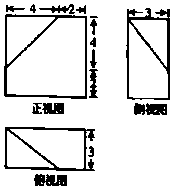

| A. | 100 | B. | 82 | C. | 96 | D. | 112 |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点在直线x=6上,其中一条渐近线方程为y=$\sqrt{3}$x,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{36}$-$\frac{{y}^{2}}{108}$=1 | B. | $\frac{{x}^{2}}{108}$-$\frac{{y}^{2}}{36}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | D. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 |
11.某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
9.欧拉公式eix=cosx+isinx (i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知,e${\;}^{\frac{π}{3}i}$表示的复数的模为( )
0 238850 238858 238864 238868 238874 238876 238880 238886 238888 238894 238900 238904 238906 238910 238916 238918 238924 238928 238930 238934 238936 238940 238942 238944 238945 238946 238948 238949 238950 238952 238954 238958 238960 238964 238966 238970 238976 238978 238984 238988 238990 238994 239000 239006 239008 239014 239018 239020 239026 239030 239036 239044 266669
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{3}$ |