18.已知两点A(-1,1),B(3,5),点C在曲线y=2x2上运动,则$\overrightarrow{AB}•\overrightarrow{AC}$的最小值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
17.已知命题p:?x∈R,x2+ax+a2≥0(a∈R),命题q:$?{x_0}∈{N^*}$,$2x_0^2-1≤0$,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (?p)∨q | D. | (?p)∧(?q) |
16.已知集合A={-1,0,1,2,3,4,5},B={b|b=n2-1,n∈Z},则A∩B=( )
| A. | {-1,3} | B. | {0,3} | C. | {-1,0,3} | D. | {-1,0,3,5} |
15.点M为椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$上一点,则M到直线的距离x+2y-10=0最小值为( )
| A. | $3\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
10. 为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):
为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):
(Ⅰ)根据上表数据在下列网格中绘制散点图;
(Ⅱ)根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
0 238840 238848 238854 238858 238864 238866 238870 238876 238878 238884 238890 238894 238896 238900 238906 238908 238914 238918 238920 238924 238926 238930 238932 238934 238935 238936 238938 238939 238940 238942 238944 238948 238950 238954 238956 238960 238966 238968 238974 238978 238980 238984 238990 238996 238998 239004 239008 239010 239016 239020 239026 239034 266669
 为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):
为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):| x | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
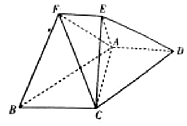 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.