13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(α>0,b>0)的左右焦点为F1,F2,|F1F2|=2$\sqrt{5}$,点P是双曲线右支上一点,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=10,在△PF1F2中,∠PF1F2的角平分线与另外两个角的外角平分线交于一点Q,Q点横坐标为4,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{15}}{3}$ |
7.设a为实数,函数f(x)=x2-2ax.
(Ⅰ)当a=1时,求f(x)在区间[0,2]上的值域;
(Ⅱ)设函数g(x)=|f(x)|,t(a)为g(x)在区间[0,2]上的最大值,求t(a)的最小值.
0 224954 224962 224968 224972 224978 224980 224984 224990 224992 224998 225004 225008 225010 225014 225020 225022 225028 225032 225034 225038 225040 225044 225046 225048 225049 225050 225052 225053 225054 225056 225058 225062 225064 225068 225070 225074 225080 225082 225088 225092 225094 225098 225104 225110 225112 225118 225122 225124 225130 225134 225140 225148 266669
(Ⅰ)当a=1时,求f(x)在区间[0,2]上的值域;
(Ⅱ)设函数g(x)=|f(x)|,t(a)为g(x)在区间[0,2]上的最大值,求t(a)的最小值.
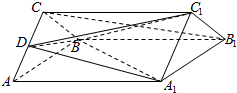 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D