11.设f(x)=$\frac{{x-\sqrt{3}}}{{\sqrt{3}x+1}}$,且满足fn(x)=f(fn-1(x)),n∈N*,若f0(x)=f(x),则f2015(0)=( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | 2015 |
9.双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点为F1、F2,以线段F1F2为边作正三角形MF1F2,若MF1的中点在双曲线上,则$\frac{{b}^{2}}{{a}^{2}}$=( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | 3+2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
8.已知直线y=k(x+2)(k>0)与焦点为F的抛物线y2=8x相交于A,B两点,若$|{\overrightarrow{AF}}|=4|{\overrightarrow{BF}}|$,则k=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
6.若实数a,b在区间[0,$\sqrt{2}$]上取值,则函数f(x)=$\frac{2}{3}$ax3+bx2+ax在R上有两个相异极值点的概率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{8}$ | D. | $\frac{1}{2}$ |
3.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2011}$的值的一个程序框图,其中判断框内应填入的条件是( )

0 224726 224734 224740 224744 224750 224752 224756 224762 224764 224770 224776 224780 224782 224786 224792 224794 224800 224804 224806 224810 224812 224816 224818 224820 224821 224822 224824 224825 224826 224828 224830 224834 224836 224840 224842 224846 224852 224854 224860 224864 224866 224870 224876 224882 224884 224890 224894 224896 224902 224906 224912 224920 266669

| A. | i≤2011 | B. | i>2011 | C. | i≤1005 | D. | i>1005 |
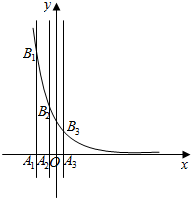 (理)已知等差数列{an}的首项为p,公差为d(d>0),对于不同的自然数n(n∈N*),直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(理)已知等差数列{an}的首项为p,公差为d(d>0),对于不同的自然数n(n∈N*),直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.