10.已知数列{an}满足a1=1,an+1=2an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn为数列{$\frac{2n}{{a}_{n}+1}$}的前n项和,求证:1≤Sn<4.
(1)求数列{an}的通项公式;
(2)设Sn为数列{$\frac{2n}{{a}_{n}+1}$}的前n项和,求证:1≤Sn<4.
8.若$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$=(1,2),$\overrightarrow{a}$+$\overrightarrow{b}$=(4,-10),则$\overrightarrow{a}$等于( )
| A. | (-2,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
6.已知偶函数f(x)在(-∞,0]上单调递减,f(-1)=0,若f(log2x)<0,则x的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
4.已知$\overrightarrow{a}$=(sinωx,1),$\overrightarrow{b}$=(1,cosωx),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$的周期为π,则f(x)的一个对称中心为( )
| A. | ($\frac{π}{4}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | (-$\frac{π}{8}$,0) |
2.将函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)的图象向左平移$\frac{3}{2}$π个单位后与原来的图象重合,且f(x)≤f(π)恒成立,则ω的值( )
0 224675 224683 224689 224693 224699 224701 224705 224711 224713 224719 224725 224729 224731 224735 224741 224743 224749 224753 224755 224759 224761 224765 224767 224769 224770 224771 224773 224774 224775 224777 224779 224783 224785 224789 224791 224795 224801 224803 224809 224813 224815 224819 224825 224831 224833 224839 224843 224845 224851 224855 224861 224869 266669
| A. | 等于$\frac{4}{3}$ | B. | 等于$\frac{3}{4}$ | C. | 等于$\frac{8}{3}$ | D. | 有很多种情况 |
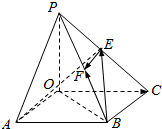 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.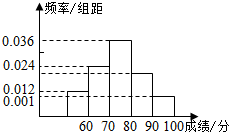 对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图:
对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图: