16.下列函数中在($\frac{π}{4}$,$\frac{3}{4}$π)上为减函数的是( )
| A. | y=-tanx | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
15.已知O是平面内任意一点,α是任意角,下列等式一定可以判定A,B,C三点共线的是( )
| A. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$+cosα$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=sin2α$\overrightarrow{OA}$+cos2α$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$-cosα$\overrightarrow{OB}$ | D. | $\overline{OC}$=sin2α$\overrightarrow{OA}$-cos2α$\overrightarrow{OB}$ |
14.下列说法中正确的是( )
| A. | 向量$\overrightarrow{a}$与非零向量$\overrightarrow{b}$共线,$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$与$\overrightarrow{c}$共线 | |
| B. | 任意两个相等向量不一定是共线向量 | |
| C. | 任意两个共线向量相等 | |
| D. | 若向量$\overrightarrow{a}$与$\overrightarrow{b}$共线,则$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ>0) |
13.下面说法正确的是( )
| A. | 平面内的任意两个向量都共线 | B. | 空间的任意三个向量都不共面 | ||
| C. | 空间的任意两个向量都共面 | D. | 空间的任意三个向量都共面 |
9.函数f(x)=|x2-a2|(α>0),动点P(m,n)满足f(m)=f(n),且m<n<0,若动点P(m,n)的轨迹直线x+y+1=0没有公共点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{\sqrt{2}}{2}$,+∞) | D. | (0,$\frac{1}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞) |
7.已知集合P={x|6<x<8},Q={x|x∈N},则P∩Q等于( )
0 224550 224558 224564 224568 224574 224576 224580 224586 224588 224594 224600 224604 224606 224610 224616 224618 224624 224628 224630 224634 224636 224640 224642 224644 224645 224646 224648 224649 224650 224652 224654 224658 224660 224664 224666 224670 224676 224678 224684 224688 224690 224694 224700 224706 224708 224714 224718 224720 224726 224730 224736 224744 266669
| A. | {7} | B. | {6,7} | C. | {6,7,8} | D. | {x|6<x<8} |
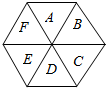 如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?
如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?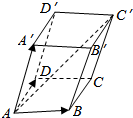 在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.
在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.