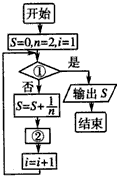
 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 108 |
| A、i>108,n=n+1 |
| B、i>108,n=n+2 |
| C、i>54,n=n+2 |
| D、i≤54,n=n+2 |
设全集U=R,A={x∈N|y=ln(2-x)},B={x|x(x-2)≤0},A∩B=( )
| A、{x|x≥1} |
| B、{x|0≤x<2} |
| C、{1} |
| D、{0,1} |
在平面直角坐标系中,记由点A(0,1),B(4,2),C(2,6)围成的三角形区域(含边界)为D,P(x,y)为区域D上的点,则
最大值与最小值的和为( )
| (x-2)2+(y-2)2 |
A、
| ||||||||
B、
| ||||||||
| C、4 | ||||||||
D、
|
若x,y满足约束条件
,则z=3x-y的取值范围是( )
|
| A、(-1,9) |
| B、[-1,9] |
| C、(1,9) |
| D、[1,9] |
已知{an}是以1为首项的等比数列,若a7•a11=100,则a9的值是( )
| A、-10 | B、10 |
| C、±10 | D、不确定 |
一个几何体按比例绘制的三视图如图所示(单位:m)
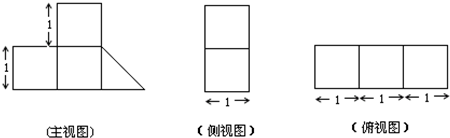
则该几何体的表面积为( )m3.

则该几何体的表面积为( )m3.
| A、14 | ||
| B、15 | ||
C、14+
| ||
D、15+
|
设
=(cosx-sinx,2sinx),
=(cosx+sinx,cosx),f(x)=
•
,将函数f(x)的图象平移而得到函数g(x)=
cos2x-1,则平移方法可以是( )
| a |
| b |
| a |
| b |
| 2 |
A、左移
| ||
B、左移
| ||
C、右移
| ||
D、左移
|
等比数列{an}中a4+a8=-2,则a42+2a62+a6a10的值为( )
| A、4 | B、5 | C、8 | D、-9 |
斐波那契数列{Fn},1,1,2,3,5,8,13,21,34,55,89,144,283,…,现已知{Fn}的连续两项平方和仍是数列{Fn}中的项,则F39+F40=( )
| A、F39 |
| B、F40 |
| C、F41 |
| D、F42 |
给出以下命题:
①?x∈R,sinx+cosx>1;
②?x∈R,x2-x+1<0;
③“x>1”是“|x|>1”充分不必要条件;
④
|cosx|dx=0.
其中假命题的个数是( )
①?x∈R,sinx+cosx>1;
②?x∈R,x2-x+1<0;
③“x>1”是“|x|>1”充分不必要条件;
④
| ∫ | π 0 |
其中假命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |