设x,y满足不等式组
则目标函数z=2x+y的最小值是( )
|
A、
| ||
| B、4 | ||
C、
| ||
D、
|
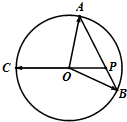 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
|
A、
| ||
| B、4 | ||
C、
| ||
D、
|
 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |