题目内容
已知函数f(x)=(
)x-(
)x(1≤x≤2)
(1)求(
)x(1≤x≤2)的取值范围;
(2)求f(x)的值域;
(3)若不等式(
)x-(
)x+a≥0在[1,2]上恒成立,求a的取值范围.
| 1 |
| 4 |
| 1 |
| 2 |
(1)求(
| 1 |
| 2 |
(2)求f(x)的值域;
(3)若不等式(
| 1 |
| 4 |
| 1 |
| 2 |
考点:函数恒成立问题,复合函数的单调性
专题:函数的性质及应用
分析:(1)利用指数函数的单调性求范围;
(2)利用换元法转化为二次函数求解;
(3)将a分离出来,然后求不等号右边的函数的最值即可.
(2)利用换元法转化为二次函数求解;
(3)将a分离出来,然后求不等号右边的函数的最值即可.
解答:
解:(1)因为y=(
)x在定义域内是减函数,结合1≤x≤2,所以(
)2≤(
)x≤(
)1,即
≤(
)x≤
.
(2)令t=(
)x∈[
,
].原函数化为:y=t2-t=(t-
)2-
.t∈[
,
],
该函数在[
,
]上是减函数,所以当t=
时ymin=-
,t=
时,ymax=-
,故f(x)的值域为[-
,-
].
(3)若(
)x-(
)x+a≥0在[1,2]上恒成立,即a≥-(
)x+(
)x=-[(
)x]2+(
)x.x∈[1,2]恒成立.
令t=(
)x∈[
,
],则a≥-t2+t=-(t-
)2+
.t∈[
,
]恒成立,显然当t=
时,-t2+t取得最大值
.
故a的范围是[
,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)令t=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
该函数在[
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
| 1 |
| 4 |
| 3 |
| 16 |
(3)若(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令t=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故a的范围是[
| 1 |
| 4 |
点评:本题考查了利用指数函数的单调性求值域,以及利用配方法求二次函数的最值的方法,不等式恒成立问题一般要转化为函数的最值问题求解.

练习册系列答案
相关题目
已知定义在(-1,1)上的函数f(x)=x-sinx,若f(a-2)+f(4-a2)<0,则a的取值范围是( )
A、(2,
| ||||
B、(
| ||||
| C、(0,2) | ||||
| D、(-∞,-1)∪(2,+∞) |
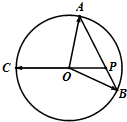 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
在△ABC中,a=x,b=2,B=45°,若该三角形有两个解,则x的取值范围是( )
| A、x>2 | ||
| B、x<2 | ||
C、2
| ||
D、2
|
不等式组
的解集记为D,由下面四个命题:
P1:?(x,y)∈D,则2x-y≥-1;
P2:?(x,y)∈D,则2x-y<-2;
P3:?(x,y)∈D,则2x-y>7;
P4:?(x,y)∈D,则2x-y≤5.
其中正确命题是( )
|
P1:?(x,y)∈D,则2x-y≥-1;
P2:?(x,y)∈D,则2x-y<-2;
P3:?(x,y)∈D,则2x-y>7;
P4:?(x,y)∈D,则2x-y≤5.
其中正确命题是( )
| A、P2,P3 |
| B、P1,P2 |
| C、P1,P3 |
| D、P1,P4 |
若A={x|log2(x-4)<1},B={y|y=3x+2,-4≤x≤3},则A∩B=( )
| A、[-10,6) |
| B、(4,6) |
| C、(6,11] |
| D、(0,11] |
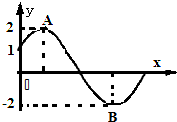 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤