(本小题满分12分)
已知椭圆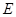 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线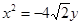 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点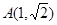 在该椭圆上.
在该椭圆上.
(1)求椭圆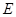 的方程;
的方程;
(2)若斜率为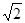 直线
直线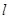 与椭圆
与椭圆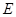 交于不同的两点
交于不同的两点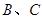 ,当
,当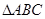 面积的最大值时,求直线
面积的最大值时,求直线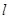 的方程.
的方程.
已知椭圆
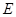 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线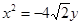 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点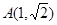 在该椭圆上.
在该椭圆上.(1)求椭圆
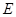 的方程;
的方程;(2)若斜率为
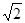 直线
直线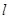 与椭圆
与椭圆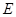 交于不同的两点
交于不同的两点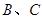 ,当
,当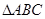 面积的最大值时,求直线
面积的最大值时,求直线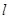 的方程.
的方程.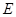 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线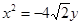 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点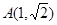 在该椭圆上.
在该椭圆上.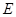 的方程;
的方程;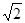 直线
直线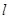 与椭圆
与椭圆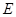 交于不同的两点
交于不同的两点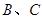 ,当
,当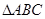 面积的最大值时,求直线
面积的最大值时,求直线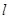 的方程.
的方程.