题目内容
(本小题满分12分)
在平面直角坐标系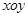 中,已知三点
中,已知三点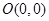 ,
,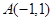 ,
, ,曲线C上任意—点
,曲线C上任意—点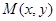 满足:
满足: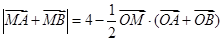 .
.
(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为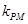 ,
,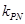 .试探究
.试探究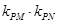 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;
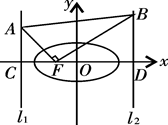
(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时,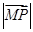 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.
在平面直角坐标系
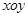 中,已知三点
中,已知三点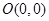 ,
,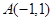 ,
, ,曲线C上任意—点
,曲线C上任意—点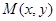 满足:
满足: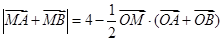 .
.(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为
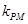 ,
,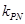 .试探究
.试探究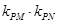 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时,
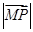 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.(l) 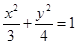 (2)
(2) 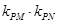
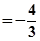 (3)
(3) 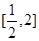
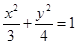 (2)
(2) 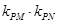
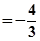 (3)
(3) 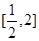
试题分析:(1)由题意可得,
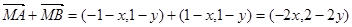 ,
,所以
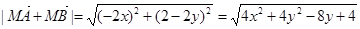 ,
, 又
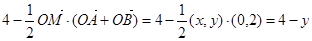 ,
, 所以
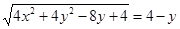 ,即
,即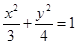 .
. (2)因为过原点的直线
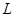 与椭圆相交的两点
与椭圆相交的两点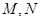 关于坐标原点对称,
关于坐标原点对称,所以可设
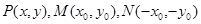 .
. 因为
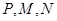 在椭圆上,所以有
在椭圆上,所以有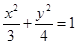 , ………①
, ………① 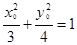 , ………②
, ………②①-②得
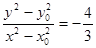 .
.又
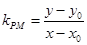 ,
,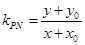 ,
, 所以
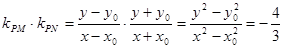 ,
, 故
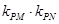 的值与点
的值与点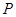 的位置无关,与直线
的位置无关,与直线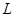 也无关.
也无关. (3)由于
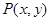 在椭圆
在椭圆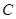 上运动,椭圆方程为
上运动,椭圆方程为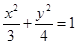 ,故
,故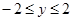 ,且
,且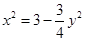 . 因为
. 因为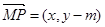 ,所以
,所以 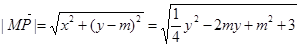
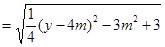 .
. 由题意,点
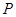 的坐标为
的坐标为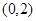 时,
时,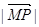 取得最小值,即当
取得最小值,即当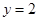 时,
时,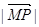 取得最
取得最 小值,而
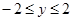 ,故有
,故有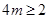 ,解得
,解得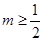 .
. 又椭圆
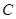 与
与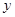 轴交于
轴交于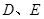 两点的坐标为
两点的坐标为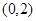 、
、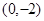 ,而点
,而点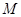 在线段
在线段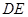 上, 即
上, 即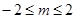 ,亦即
,亦即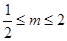 ,所以实数
,所以实数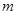 的取值范围是
的取值范围是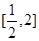 .
.点评:求轨迹方程的大体步骤:1建立直角坐标系,设出动点坐标,2找到关于动点的关系式,3关系式坐标化,整理化简,4除去不满足题意要求的个别点。本题第二三小题较复杂,学生很难达到满分

练习册系列答案
相关题目
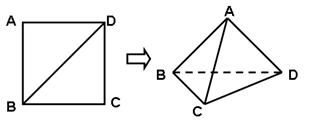
 ABD为二面角A-BC-D的平面角;(2)AC
ABD为二面角A-BC-D的平面角;(2)AC BD;(3) △ACD是等边三角形;
BD;(3) △ACD是等边三角形;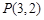 且与双曲线
且与双曲线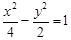 有相同渐近线方程的双曲线的标准方程为 .
有相同渐近线方程的双曲线的标准方程为 .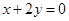 与圆
与圆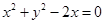 的交点为A、B,
的交点为A、B,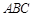 的两个顶点
的两个顶点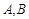 的坐标分别是
的坐标分别是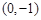 ,
,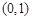 ,且
,且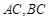 所在直线的斜率之积等于
所在直线的斜率之积等于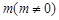 .
.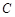 的轨迹
的轨迹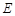 的方程,并判断轨迹
的方程,并判断轨迹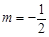 时,过点
时,过点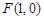 的直线
的直线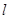 交曲线
交曲线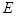 于
于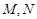 两点,设点
两点,设点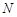 关于
关于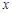 轴的对称点为
轴的对称点为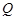 (
(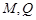 不重合).求证直线
不重合).求证直线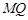 与
与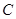 的两焦点是
的两焦点是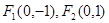 ,离心率
,离心率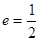 .
.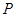 在椭圆
在椭圆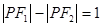 ,求DPF1F2的面积.
,求DPF1F2的面积.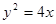 上一个动点,Q为圆
上一个动点,Q为圆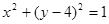 上一个动点,那么点P到点Q的距离与点P到
上一个动点,那么点P到点Q的距离与点P到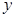 轴距离之和最小值是( )
轴距离之和最小值是( )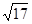
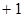
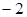
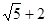
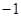
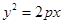 的焦点与双曲线
的焦点与双曲线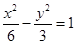 的右焦点重合,则
的右焦点重合,则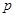 的值 .
的值 .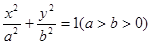 的左、右准线分别为
的左、右准线分别为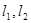 ,且分别交
,且分别交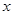 轴于
轴于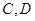 两点,从
两点,从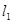 上一点
上一点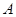 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点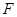 被
被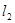 交于点
交于点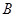 ,若
,若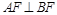 ,且
,且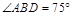 ,则椭圆的离心率等于 .
,则椭圆的离心率等于 .