给出命题:若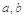 是正常数,且
是正常数,且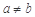 ,
,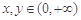 ,则
,则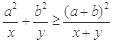 (当且仅当
(当且仅当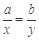 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数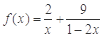 (
(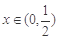 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.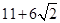 , ,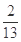 | B.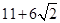 , ,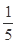 |
C.25,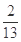 | D.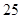 , ,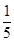 |
用数学归纳法证明:“1+a+a2+ +an+1= (a≠1,n∈N*)”在验证n=1时,左端计算所得的项为( )
(a≠1,n∈N*)”在验证n=1时,左端计算所得的项为( )
| A.1 | B.1+a |
| C.1+a+a2 | D.1+a+a2+a3 |
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左往右数第
行,从左往右数第 个数,若
个数,若 ,则
,则 与
与 的和为( )
的和为( )
| A.105 | B.103 | C.82 | D.81 |
设 则
则 ( )
( )
A.都不大于 |
B.都不小于 |
C.至少有一个不大于 |
D.至少有一个不小于 |
有一段 “三段论”推理是这样的:对于可导函数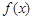 ,若
,若 ,则
,则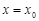 是函数
是函数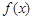 的极值点.因为
的极值点.因为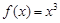 在
在 处的导数值
处的导数值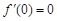 ,所以
,所以 是
是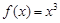 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
有一段 “三段论”推理是这样的:对于可导函数 ,若
,若 ,则
,则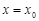 是函数
是函数 的极值点.因为
的极值点.因为 在
在 处的导数值
处的导数值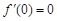 ,所以
,所以 是
是 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线 直线
直线 ”结论显然是错误的,这是因为( )
”结论显然是错误的,这是因为( )
| A.大前提错误 | B.推理形式错误 | C.小前提错误 | D.非以上错误 |
用数学归纳法证明1+ +
+ +…+
+…+ =-
=- (
( ≠1,n∈N*),在验证n=1成立时,左边的项是( )
≠1,n∈N*),在验证n=1成立时,左边的项是( )
| A.1 | B.1+ | C.1+ + + | D.1+ + + + + |
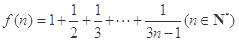 ,则对于
,则对于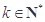 ,
,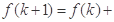 .
.