题目内容
有一段 “三段论”推理是这样的:对于可导函数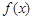 ,若
,若 ,则
,则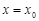 是函数
是函数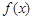 的极值点.因为
的极值点.因为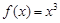 在
在 处的导数值
处的导数值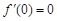 ,所以
,所以 是
是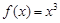 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
A
解析试题分析:∵大前提是:“对于可导函数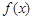 ,如果
,如果 ,那么
,那么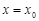 是函数
是函数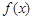 的极值点”,不是真命题,因为对于可导函数
的极值点”,不是真命题,因为对于可导函数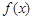 ,如果
,如果 ,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.
,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.
考点:演绎推理的基本方法.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知 (
( ),计算得
),计算得 ,
, ,
, ,
, ,
, ,由此推算:当
,由此推算:当 时,有( )
时,有( )
A. ( ( ) ) |
B. ( ( ) ) |
C. ( ( ) ) |
D. ( ( ) ) |
给出命题:若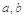 是正常数,且
是正常数,且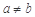 ,
,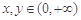 ,则
,则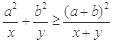 (当且仅当
(当且仅当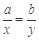 时等号成立).根据上面命题,可以得到函数
时等号成立).根据上面命题,可以得到函数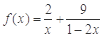 (
(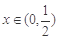 )的最小值及取最小值时的
)的最小值及取最小值时的 值分别为( )
值分别为( )
A.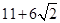 , ,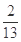 | B.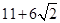 , ,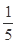 |
C.25,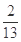 | D.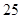 , ,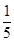 |
用数学归纳法证明“ ”(
”( )时,从 “
)时,从 “ ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )
A. | B. | C. | D.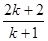 |
用反证法证明命题“三角形的内角至少有一个不大于60°”时,应该先
| A.假设三内角都不大于60° |
| B.假设三内角都大于60° |
| C.假设三内角至多有一个大于60° |
| D.假设三内角至多有两个大于60° |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
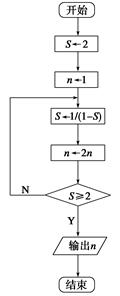
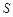 的值为
的值为 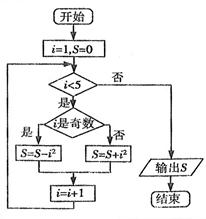
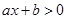 (
(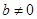 )的程序框图.
)的程序框图.