题目内容
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左往右数第
行,从左往右数第 个数,若
个数,若 ,则
,则 与
与 的和为( )
的和为( )
| A.105 | B.103 | C.82 | D.81 |
D
解析试题分析:由三角形数表可以看出其奇数行为奇数列,偶数行为偶数列,由2013=2×1007﹣1,得2013为第1007个奇数,又前31个奇数行内数的个数的和为1+3+…+61=961,前32个奇数行内数的个数的和为1024,故2013在第32个奇数行内,所以i=63,且奇数从大到小排列,因为第63行的第一个数为2×1024﹣1=2047,2013=2047﹣2(m﹣1),所以m=18,即j=18,所以i+j=81.故选D
考点:简单的演绎推理;数列的特点; 等差数列与等比数列.

练习册系列答案
相关题目
用数学归纳法证明1+ +
+ +…+
+…+ =-
=- (
( ≠1,n∈N*),在验证n=1成立时,左边的项是( )
≠1,n∈N*),在验证n=1成立时,左边的项是( )
| A.1 | B.1+ | C.1+ + + | D.1+ + + + + |
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且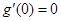 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
推理:因为平行四边形对边平行且相等,而矩形是特殊的平行四边形,所以矩形的对边平行且相等.以上推理的方法是( )
| A.合情推理 | B.演绎推理 | C.归纳推理 | D.类比推理 |
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
| A.(7,5) | B.(5,7) | C.(2,10) | D.(10,1) |

 在
在 方向上的投影.
方向上的投影.  的值为
的值为 ,则输出
,则输出 的值为______.
的值为______.
 =2,则输出的数等于________.
=2,则输出的数等于________.