在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.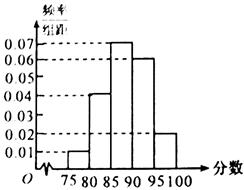
(1)下表是这次抽查成绩的频数分布表,试求正整数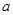 、
、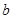 的值;
的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
空气质量指数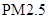 (单位:
(单位: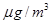 )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
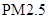 日均浓度 日均浓度 |  | 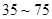 | 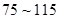 | 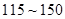 | 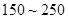 |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
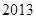 年
年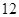 月
月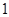 日—
日—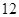 月
月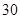 日(
日(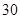 天)对空气质量指数
天)对空气质量指数 进行监测,获得数据后得到如下条形图.
进行监测,获得数据后得到如下条形图. 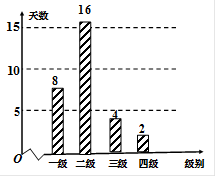
(1)估计该城市一个月内空气质量类别为优的概率;
(2)从空气质量级别为三级和四级的数据中任取
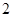 个,求恰好有一天空气质量类别为中度污染的概率.
个,求恰好有一天空气质量类别为中度污染的概率.
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 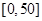 | 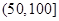 | 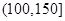 | 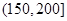 |  | 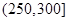 | 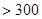 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面
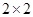 列联表,并判断能否有
列联表,并判断能否有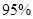 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
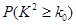 | 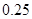 | 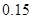 | 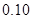 | 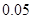 | 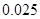 | 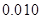 |  | 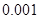 |
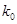 | 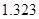 | 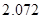 | 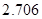 | 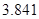 |  | 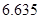 | 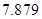 | 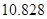 |
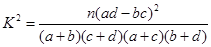
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
某电视台举办青年歌手大奖赛,有10名评委打分,已知甲、乙两名选手演唱后的打分情况如茎叶图所示:
| 甲 | | 乙 |
| 6 4 3 | 9 | 1 5 |
| 8 7 7 5 4 2 | 8 | 0 1 3 6 6 8 8 9 |
| 9 | 7 | |
(2)现场有3名点评嘉宾A、B、C,每位选手可以从中选2位进行指导,若选手选每位点评嘉宾的可能性相等,求甲乙两选手选择的点评嘉宾恰重复一人的概率.
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
(2)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
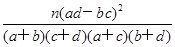 . ?
. ?临界值表
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲组 | 4 | 5 | x | 9 | 10 |
| 乙组 | 5 | 6 | 7 | y | 9 |
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
 的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:
的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位: ).
).
 .
. 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.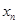 表示编号为
表示编号为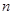 (
(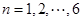 )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差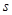 ;
; 表示编号为
表示编号为 (
( )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72. ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
; 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下 段:
段:
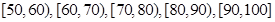 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
 的频率;
的频率; 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求