题目内容
某校高一年级
名学生参加数学竞赛，成绩全部在
分至
分之间，现将成绩分成以下
段：
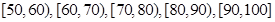，据此绘制了如图所示的频率分布直方图. 
（1）求成绩在区间
的频率；
（2）从成绩大于等于
分的学生中随机选
名学生，其中成绩在
内的学生人数为
，求的分布列与均值.
（1）
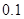；（2）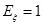
.
解析试题分析：（1）根据频率分布直方图可知成绩在区间的频率为
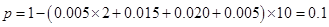；（2）由已知和（1）的结果可知成绩在区间内的学生有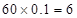
人，成绩在区间
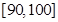内的学生有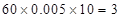
人，那么的所有可能取值为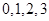
，然后求出所对应的概率分别为：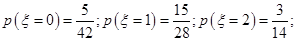
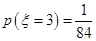，列出分布列后求出的数学期望为：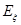
=
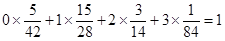
试题解析：（1）根据频率分布直方图可知成绩在区间的频率为；
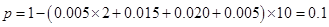（2）由已知和（1）的结果可知成绩在区间内的学生有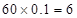人，成绩在区间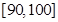内的学生有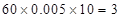人， 依题意，可能取的值为.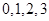
则：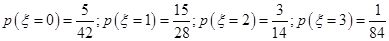 
所以的分布列为：
则均值0 1 2 3 P 
=
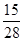
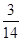
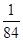
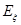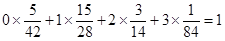
考点：频率分布直方图，离散型随机变量的分布列与数学期望.
练习册系列答案
相关题目
城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间作为样本分成5组，如下表所示（单位：分钟）：
| 组别 | 候车时间 | 人数 |
| 一 |  | 2 |
| 二 |  | 6 |
| 三 |  | 4 |
| 四 |  | 2 |
| 五 |  | 1 |
（2）若从上表第三、四组的6人中任选2人作进一步的调查，求抽到的两人恰好来自不同组的概率．
某地粮食需求量逐年上升,下表是部分统计数据:
| 年份(年) | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量 (万吨) | 236 | 246 | 257 | 276 | 286 |
=
x+
.(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
，求恰有一名同学获得该高校B类资格的概率．
的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下（单位：
）.
.
的值，并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
