题目内容
在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.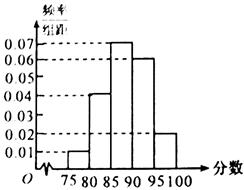
(1)下表是这次抽查成绩的频数分布表,试求正整数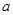 、
、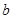 的值;
的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
(1) ;(2)
;(2) 人;(3)数学期望为
人;(3)数学期望为 .
.
解析试题分析:(1)从所给出的频率分布直方图中可知80分至85分所占的频率为 ,那么
,那么 ;95分至100分所占的频率为
;95分至100分所占的频率为 ,所以
,所以 .(2)根据分层抽样可以得到抽取成绩为优秀的学生人数为30人;(3)优秀人数X的所有可能取值分别为
.(2)根据分层抽样可以得到抽取成绩为优秀的学生人数为30人;(3)优秀人数X的所有可能取值分别为 人,
人, 人,
人, 人.先计算出
人.先计算出 ,那么可以列出其分布列,然后计算出所对应的数学期望
,那么可以列出其分布列,然后计算出所对应的数学期望 .
.
试题解析:(1)80分至85分的人数为: (人);
(人);
95分至100分的人数为: (人);
(人);
(2)用分层抽样的方法从1000人中抽取40人,其中成绩为优秀的学生人数为: (人);
(人);
(3)在抽取的40人中,85分以下的共有10人,85分及其以上的共有30人,从中抽取的2人中,
成绩优秀的人数X的可能取值分别是:0人、1人、2人,其分布列如下表:
X的数学期望为:X 0 1 2 P(X) 



考点:频率分布直方图;离散型随机变量的分布列;数学期望.

 阅读快车系列答案
阅读快车系列答案下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 =bx+a.
=bx+a.(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
为了解某市民众对政府出台楼市限购令的情况,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令赞成的人数如下表:
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令?
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |
附:K2=
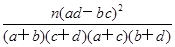
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 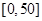 | 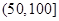 | 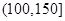 | 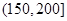 |  | 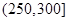 | 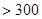 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面
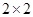 列联表,并判断能否有
列联表,并判断能否有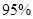 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
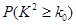 | 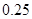 | 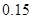 | 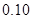 | 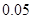 | 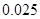 | 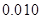 |  | 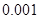 |
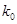 | 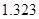 | 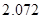 | 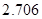 | 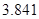 |  | 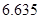 | 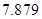 | 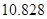 |
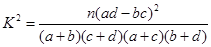
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见下表:
日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见下表:
 日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
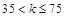 | 二级 |
 | 超标 |

某环保部门为了了解甲、乙两市的空气质量状况,在某月中分别随机抽取了甲、乙两市6天的
 日均值作为样本,样本数据茎叶图如右图所示(十位为茎,个位为叶).
日均值作为样本,样本数据茎叶图如右图所示(十位为茎,个位为叶).(1)求甲、乙两市
 日均值的样本平均数,据此判断该月中哪个市的空气质量较好;
日均值的样本平均数,据此判断该月中哪个市的空气质量较好;(2)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量等级为一级的概率.
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
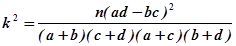 )其中n=a+b+c+d
)其中n=a+b+c+d 
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 ,第2组
,第2组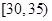 ,第3组
,第3组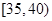 ,第4组
,第4组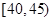 ,第5组
,第5组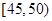 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.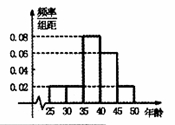

 的值;
的值; ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)