题目内容
空气质量指数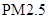 (单位:
(单位: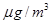 )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
 日均浓度 日均浓度 |  | 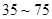 | 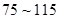 | 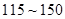 | 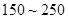 |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
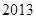 年
年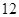 月
月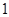 日—
日—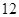 月
月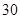 日(
日(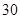 天)对空气质量指数
天)对空气质量指数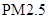 进行监测,获得数据后得到如下条形图.
进行监测,获得数据后得到如下条形图. 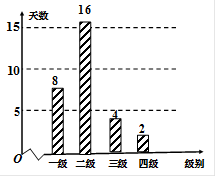
(1)估计该城市一个月内空气质量类别为优的概率;
(2)从空气质量级别为三级和四级的数据中任取
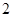 个,求恰好有一天空气质量类别为中度污染的概率.
个,求恰好有一天空气质量类别为中度污染的概率.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由条形统计图可知,空间质量类别为优的天数为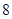 天,那么一个月内空气质量为优的概率为
天,那么一个月内空气质量为优的概率为 ;(2)样本中空气质量级别为三级的有4天,设其编号为
;(2)样本中空气质量级别为三级的有4天,设其编号为 ;样本中空气质量级别为四级的有2天,设其编号为
;样本中空气质量级别为四级的有2天,设其编号为 ,空气质量为三级的有
,空气质量为三级的有 天,空气质量为四级的有
天,空气质量为四级的有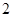 天,则基本事件总数为
天,则基本事件总数为 个:
个: ;
; ;
; ;
; ;
; .恰好有
.恰好有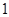 天空气质量类别为中度污染的事件共
天空气质量类别为中度污染的事件共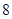 个,那么所对应的概率为
个,那么所对应的概率为 .
.
试题解析:(1)由条形统计图可知,空气质量类别为优的天数为8天,
所以此次监测结果中空气质量类别为优的概率为 .
.
(2)样本中空气质量级别为三级的有4天,设其编号为 ;
;
样本中空气质量级别为四级的有2天,设其编号为
则基本事件有: ;
; ;
; ;
; ;
; .共15个.
.共15个.
其中恰好有1天空气质量类别为中度污染的情况为:
 共8个
共8个
所以恰好有1天空气质量类别为中度污染的概率为 .
.
考点:频率分布直方图;古典概型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
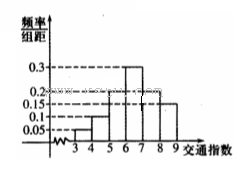
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
| API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
| 级 别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状 况 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| |  |  |  |  |  | ||

(1)求直方图中x的值.
(2)计算一年中空气质量分别为良和轻微污染的天数.
(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
(结果用分数表示.
已知57=78125,27=128,
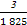 +
+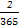 +
+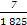 +
+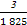 +
+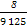 =
=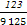 ,365=73×5).
,365=73×5). 设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=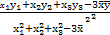 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
(2)若|yi-(
 xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率. 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
| | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲组 | 4 | 5 | x | 9 | 10 |
| 乙组 | 5 | 6 | 7 | y | 9 |
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
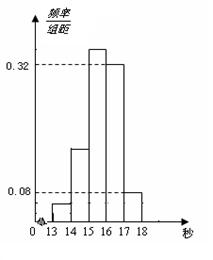

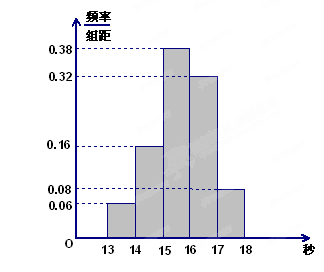
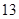 秒与
秒与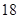 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组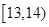 ,第二组
,第二组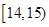 ,…,第五组
,…,第五组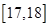 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.