已知定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足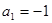 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. | B. | C. | D. |
定义在 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 ( )
( )
A. | B. | C. | D. |
已知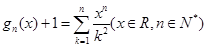 ,则下列说法正确的是( )
,则下列说法正确的是( )
①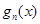 关于点
关于点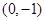 成中心对称
成中心对称
②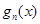 在
在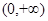 单调递增
单调递增
③当 取遍
取遍 中所有数时不可能存在
中所有数时不可能存在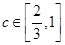 使得
使得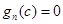
| A.①②③ | B.②③ | C.①③ | D.② |
定义在R上的函数 具有下列性质:①
具有下列性质:① ;②
;② ;③
;③ 在
在 上为增函数,则对于下述命题:
上为增函数,则对于下述命题:
① 为周期函数且最小正周期为4;
为周期函数且最小正周期为4;
② 的图像关于
的图像关于 轴对称且对称轴只有1条;
轴对称且对称轴只有1条;
③ 在
在 上为减函数.
上为减函数.
正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
命题 函数
函数 在区间
在区间 上是增函数;命题
上是增函数;命题
 函数的值域为R.则
函数的值域为R.则 是
是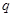 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知函数 ,
, 是方程
是方程 的两个实根,其中
的两个实根,其中 ,则实数
,则实数 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
 ( ).
( ). 的图象关于
的图象关于 ,使
,使
 时,
时, 成立,则
成立,则 的最大值为( )
的最大值为( )


 ,则函数
,则函数 的图像大致形状是( )
的图像大致形状是( )
 的图像大致是( )
的图像大致是( )


