题目内容
定义在 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 ( )
( )
A. | B. | C. | D. |
C
解析试题分析:因为 ,所以
,所以 ,从而
,从而 ,则由已知有:
,则由已知有:

 ,故选C.
,故选C.
考点:1.函数的奇偶性;2.函数的周期性.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,若
,若 在
在 上单调递减,则
上单调递减,则 在
在 上是( )
上是( )
| A.增函数 | B.减函数 |
| C.先增后减的函数 | D.先减后增的函数 |
方程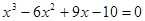 的实根个数为( )
的实根个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足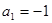 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. | B. | C. | D. |
已知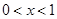 ,则
,则 取得最大值时
取得最大值时 的值为( )
的值为( )
A. | B. | C. | D.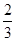 |
已知函数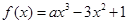 ,若
,若 存在唯一的零点
存在唯一的零点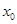 ,且
,且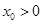 ,则
,则 的取值范围是( ).
的取值范围是( ).
A.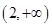 | B.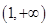 | C.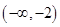 | D.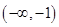 |
已知定义在R上的函数f(x)的周期为4,且当x∈(-1,3]时,f(x)=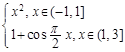 ,则函数
,则函数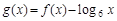 的零点个数是( )
的零点个数是( )
| A.4 | B.5 | C.6 | D.7 |
 ,
, ”的否定是:“不存在
”的否定是:“不存在 ”;
”; 的零点在区间
的零点在区间 内;
内;  的图象的切线的斜率的最大值是
的图象的切线的斜率的最大值是 ;
; 恒过样本中心
恒过样本中心 ,且至少过一个样本点.
,且至少过一个样本点.
 ”.
”. 的取值范围.
的取值范围.