题目内容
已知函数 与函数
与函数 的图象关于
的图象关于 轴对称,若存在
轴对称,若存在 ,使
,使
 时,
时, 成立,则
成立,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
C
解析试题分析:由于函数 与函数
与函数 的图象关于
的图象关于 轴对称,因此
轴对称,因此 ,由
,由 得
得 ,把
,把 代入得
代入得 ,当
,当 时,
时, ,
,
解之得 ,因此
,因此 的最大值为
的最大值为 .
.
考点:函数图象的对称性.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数f(x)是偶函数,在 上导数
上导数 >0恒成立,则下列不等式成立的是( ).
>0恒成立,则下列不等式成立的是( ).
| A.f(-3)<f(-1)<f(2) | B.f(-1)<f(2)<f(-3) |
| C.f(2)<f(-3)<f(-1) | D.f(2)<f(-1)<f(-3) |
已知函数 的图像如图所示,则
的图像如图所示,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
定义在R上的函数 具有下列性质:①
具有下列性质:① ;②
;② ;③
;③ 在
在 上为增函数,则对于下述命题:
上为增函数,则对于下述命题:
① 为周期函数且最小正周期为4;
为周期函数且最小正周期为4;
② 的图像关于
的图像关于 轴对称且对称轴只有1条;
轴对称且对称轴只有1条;
③ 在
在 上为减函数.
上为减函数.
正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知 ,则下列不等式一定成立的是( ).
,则下列不等式一定成立的是( ).
A. | B. | C. | D. |
 若
若 是
是 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )
| A.[0,2] | B.[-1,2] | C.[1,2] | D.[-1,0] |
对任意实数 ,记
,记 ,若
,若 ,其中奇函数
,其中奇函数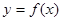 在
在 时有极小值
时有极小值 ,
, 是正比例函数,
是正比例函数, 与
与 图象如图,则下列关于
图象如图,则下列关于 的说法中正确的是( )
的说法中正确的是( )
A. 是奇函数 是奇函数 |
B. 有极大值 有极大值 和极小值 和极小值 |
C. 的最小值为 的最小值为 ,最大值为2 ,最大值为2 |
D. 在 在 上是增函数 上是增函数 |
 的图象可能是( )
的图象可能是( )
 若命题
若命题 在
在 内单调递增,如果“
内单调递增,如果“ ”
”  为真命题,“
为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围。
的取值范围。