题目内容
已知定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足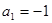 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. | B. | C. | D. |
C
解析试题分析:由定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 知,
知, =
= =
= =
= ,所以
,所以 =
=  =
=  =
=  =
= ,所以
,所以 的周期为3,由
的周期为3,由 得,
得, ,当n≥2时,
,当n≥2时, =
= ,所以
,所以 =
= ,所以
,所以 =-3,
=-3, =-7,
=-7,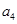 =-15,
=-15, =-31,
=-31, =-63,所以
=-63,所以
 =
= =
= =
= =3,故选C.
=3,故选C.
考点:函数的奇偶性、周期性,数列的递推公式,转化与化归思想

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知函数 ,定义如下:当
,定义如下:当 时,
时, ( ).
( ).
| A.有最大值1,无最小值 | B.有最小值0,无最大值 |
| C.有最小值—1,无最大值 | D.无最小值,也无最大值 |
定义域为R的函数 满足
满足 ,当
,当 [0,2)时
[0,2)时 若
若 时,
时, 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[-2,0) (0,l) (0,l) | B.[-2,0) [l,+∞) [l,+∞) |
| C.[-2,l] | D.( ,-2] ,-2] (0,l] (0,l] |
定义在 上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 ( )
( )
A. | B. | C. | D. |
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则 =( )
=( )
A.- | B.- | C. | D. |
已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当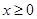 时
时 (m为常数),则
(m为常数),则 的值为( ).
的值为( ).
A. | B.6 | C.4 | D. |

 ,q:
,q:  (m>0),若
(m>0),若 是
是 的充分而不必要条件,求实数m的取值范围..
的充分而不必要条件,求实数m的取值范围..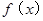 是以
是以 为周期的偶函数,当
为周期的偶函数,当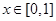 时,
时,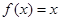 ,那么在区间
,那么在区间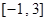 内,关于
内,关于 的方程
的方程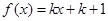 (
(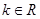 且
且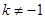 )有
)有 个不同的根,则
个不同的根,则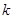 的取值范围是( )
的取值范围是( )