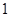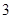设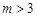 ,对于数列
,对于数列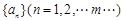 ,令
,令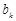 为
为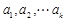 中的最大值,称数列
中的最大值,称数列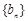 为
为 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列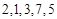 的递进上限数列为2,2,3,7,7.则下面命题中( )
的递进上限数列为2,2,3,7,7.则下面命题中( )
①若数列 满足
满足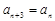 ,则数列
,则数列 的递进上限数列必是常数列
的递进上限数列必是常数列
②等差数列 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
下列命题中正确的是( )
A.命题“若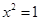 ,则 ,则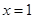 ”的否命题为“若 ”的否命题为“若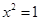 ,则 ,则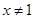 ” ” |
B.“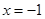 ”是“ ”是“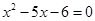 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“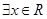 ,使得 ,使得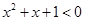 ”的否定是“ ”的否定是“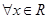 ,均有 ,均有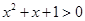 ” ” |
D.命题“在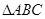 中,若 中,若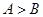 ,则 ,则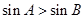 ”的逆否命题为真命题 ”的逆否命题为真命题 |
对于函数 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A. | B. |
C. | D. |
已知p:“x2+ y2 +2x=F为一圆的方程(F∈R)”,q:“F>0”,则p是q的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
可导函数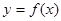 在一点的导数值为
在一点的导数值为 是函数
是函数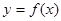 在这点取极值的( )
在这点取极值的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出如下四个命题:
①若“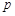 且
且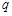 ”为假命题,则
”为假命题,则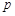 、
、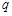 均为假命题;
均为假命题;
②命题“若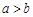 ,则
,则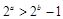 ”的否命题为“若
”的否命题为“若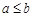 ,则
,则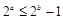 ”;
”;
③“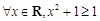 ”的否定是“
”的否定是“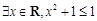 ”;
”;
④等比数列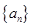 中,首项
中,首项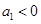 ,则数列
,则数列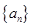 是递减数列的充要条件是公比
是递减数列的充要条件是公比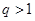 ;
;
其中不正确的命题个数是
| A.4 | B.3 | C.2 | D.1 |
“a = 1”是“复数 (
( ,i为虚数单位)是纯虚数”的( )
,i为虚数单位)是纯虚数”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
 ,且
,且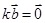 ,则
,则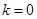 或
或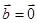 ,
,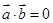 ,则
,则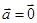 或
或 ,满足
,满足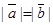 ,则
,则
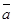 与
与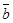 平行,则
平行,则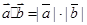 其中真命题的个数是( )
其中真命题的个数是( )