题目内容
下列命题中正确的是( )
A.命题“若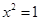 ,则 ,则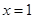 ”的否命题为“若 ”的否命题为“若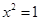 ,则 ,则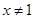 ” ” |
B.“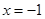 ”是“ ”是“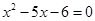 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“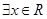 ,使得 ,使得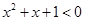 ”的否定是“ ”的否定是“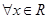 ,均有 ,均有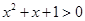 ” ” |
D.命题“在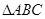 中,若 中,若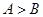 ,则 ,则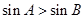 ”的逆否命题为真命题 ”的逆否命题为真命题 |
D
解析试题分析:否命题需将条件和结论分别否定,因此A项错误;由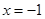 可得
可得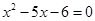 成立,因此B项为充分不必要条件;C项中
成立,因此B项为充分不必要条件;C项中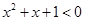 的否定是
的否定是 ,因此C错误
,因此C错误
考点:四种命题及条件关系
点评:命题的否命题需将条件和结论分别否定,原命题与逆否命题的真假相同;特称命题的否定是全称命题,需对结论加以否定,

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
“ ”是“函数
”是“函数 在区间
在区间 上为增函数”的( )
上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若 ,
, 是两个非零向量,则“
是两个非零向量,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
已知 ,
, ,
, ,
, 为实数,且
为实数,且 >
> .则“
.则“ >
> ”是“
”是“ -
- >
> -
- ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出如下四个命题:
①若“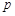 且
且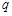 ”为假命题,则
”为假命题,则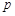 、
、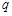 均为假命题;
均为假命题;
②命题“若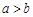 ,则
,则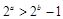 ”的否命题为“若
”的否命题为“若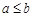 ,则
,则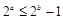 ”;
”;
③“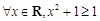 ”的否定是“
”的否定是“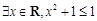 ”;
”;
④等比数列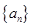 中,首项
中,首项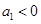 ,则数列
,则数列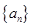 是递减数列的充要条件是公比
是递减数列的充要条件是公比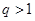 ;
;
其中不正确的命题个数是
| A.4 | B.3 | C.2 | D.1 |
“ ”是“函数
”是“函数 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“若△ABC不是等腰三角形,则它的任何两个内角不相等.”的逆否命题是( )
| A.“若△ABC是等腰三角形,则它的任何两个内角相等” |
| B.“若△ABC任何两个内角不相等,则它不是等腰三角形” |
| C.“若△ABC有两个内角相等,则它是等腰三角形” |
| D.“若△ABC任何两个角相等,则它是等腰三角形” |
“ ”是“直线
”是“直线 垂直”的
垂直”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若向量a=(x,3)(x∈R),则“x=4”是“|a|=5”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |