题目内容
可导函数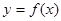 在一点的导数值为
在一点的导数值为 是函数
是函数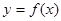 在这点取极值的( )
在这点取极值的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:以y=|x|为例,其在x=o处取到极值,但,函数在该点的导数不存在。可导函数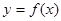 在一点的导数值为
在一点的导数值为 是函数
是函数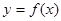 在这点取极值的必要不充分条件。选B。
在这点取极值的必要不充分条件。选B。
考点:本题主要考查应用导数研究函数的极值,函数极值存在的条件。
点评:简单题,可导函数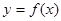 在一点的导数值为
在一点的导数值为 是函数
是函数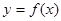 在这点取极值的必要不充分条件。
在这点取极值的必要不充分条件。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列选项叙述错误的是( )
| A.命题“若x≠l,则x2-3x十2≠0”的逆否命题是“若x2-3x十2=0,则x=1” |
B.若命题p: x x R,x2+x十1≠0,则 R,x2+x十1≠0,则 p: p: R,x2+x十1=0 R,x2+x十1=0 |
C.若p q为真命题,则p,q均为真命题 q为真命题,则p,q均为真命题 |
| D.“x>2”是“x2一3x+2>0”的充分不必要条件 |
已知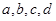 是实数,则“
是实数,则“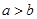 且
且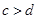 ”是“
”是“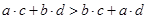 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出下面结论:
(1)命题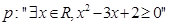 的否定为
的否定为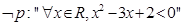 ;
;
(2)若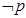 是
是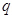 的必要不充分条件,则
的必要不充分条件,则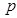 是
是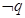 的充分不必要条件;
的充分不必要条件;
(3)“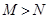 ”是“
”是“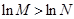 ”成立的充分不必要条件;
”成立的充分不必要条件;
(4) 若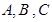 是
是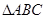 的三个内角,则“
的三个内角,则“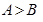 ”是“
”是“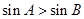 ”成立的充要条件。
”成立的充要条件。
其中正确结论的个数是
| A.4 | B.3 | C.2 | D.1 |
“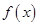 在[a,b]上为单调函数”是“函数
在[a,b]上为单调函数”是“函数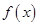 在[a,b]上有最大值和最小值”的( )
在[a,b]上有最大值和最小值”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也非必要条件 |
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题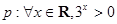 ,则( )
,则( )
A.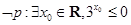 | B.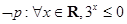 |
C. | D.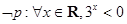 |
已知三个命题:①方程x2-x+2=0的判别式小于或等于零;②若|x|≥0,则x≥0;③5>2且3<7.其中真命题是
| A.①和② | B.①和③ | C.②和③ | D.只有① |
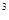 >0; ④.?x∈R,2x>0
>0; ④.?x∈R,2x>0