题目内容
14.已知直线l1:ax+y-1=0,l2:(a-2)x+ay-3=0;命题p:a=1;命题q:l1⊥l2;则命题p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 由直线的垂直关系可得a的值,由集合的包含关系可得.
解答 解:命题q,由l1⊥l2可得a(a-2)+a=0,解得a=0或a=1,
由{1}是{0,1}的真子集可得p是q的充分不必要条件
故选:A
点评 本题考查充要条件的判定,涉及直线的垂直关系,属基础题.

练习册系列答案
相关题目
7.用反证法证明“如果a<b,那么$\root{3}{a}<\root{3}{b}$”时,假设的内容应是( )
| A. | a>b | B. | $\root{3}{a}>\root{3}{b}$ | C. | $\root{3}{a}=\root{3}{b}$且$\root{3}{a}>\root{3}{b}$ | D. | $\root{3}{a}=\root{3}{b}$或$\root{3}{a}>\root{3}{b}$ |
2.设集合S={y|y=2x,x∈R},T={(x,y)|y=x2+1,x∈R},则S∩T是( )
| A. | ∅ | B. | {0} | C. | {(0,1)}和{(1,2)} | D. | {1} |
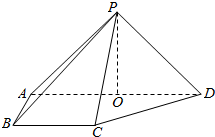 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.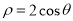 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).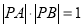 ,求实数m的值.
,求实数m的值.