题目内容
已知角θ的终边上有一点P(x,-1)(x≠0),且tanθ=-x,
(1)求sinθ,cosθ的值.
(2)求
的值.
(1)求sinθ,cosθ的值.
(2)求
| sin2θ+2sinθcosθ |
| 3sin2θ+cos2θ |
考点:同角三角函数基本关系的运用,任意角的三角函数的定义
专题:三角函数的求值
分析:(1)依题意,可得tanθ=-
=-x,可求得x=±1,从而可得sinθ,cosθ的值;
(2)当x=1时,tanθ=-1时,将所求关系式中的“弦”化“切”;当x=-1时,tanθ=1,同理可求.
| 1 |
| x |
(2)当x=1时,tanθ=-1时,将所求关系式中的“弦”化“切”;当x=-1时,tanθ=1,同理可求.
解答:
解:(1)∵θ的终边过点(x,-1)(x≠0),
∴tanθ=-
,又tanθ=-x,∴x2=1,∴x=±1.
当x=1时,sinθ=-
,cosθ=
;
当x=-1时,sinθ=-
,cosθ=-
.
(2)当x=1时,tanθ=-1,
=
=-
.
当x=-1时,tanθ=1,
=
=
.
∴tanθ=-
| 1 |
| x |
当x=1时,sinθ=-
| ||
| 2 |
| ||
| 2 |
当x=-1时,sinθ=-
| ||
| 2 |
| ||
| 2 |
(2)当x=1时,tanθ=-1,
| sin2θ+2sinθcosθ |
| 3sin2θ+cos2θ |
| tan2θ+2tanθ |
| 3tan2θ+1 |
| 1 |
| 4 |
当x=-1时,tanθ=1,
| sin2θ+2sinθcosθ |
| 3sin2θ+cos2θ |
| tan2θ+2tanθ |
| 3tan2θ+1 |
| 3 |
| 4 |
点评:本题考查同角三角函数基本关系的运用,考查转化思想与运算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
如图,已知四边形ABCD的直观图是一个边长为1的正方形,则原图形的周长为( )


A、2
| ||
| B、6 | ||
| C、8 | ||
D、4
|
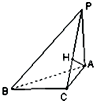 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.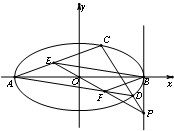 如图,在平面直角坐标系xOy中,A、B分别是椭圆:
如图,在平面直角坐标系xOy中,A、B分别是椭圆: