题目内容
在等差数列{an}，a1=-2011，其前n项和为Sn，若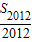
-
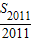=1，则S2013=（ ）A．-2012
B．-2013
C．2012
D．2013
【答案】分析：设等差数列前n项和为Sn=An2+Bn，根据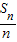
=An+B，可知{
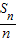}成等差数列，然后求出
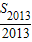的值，从而可求出所求．
解答：解：设等差数列前n项和为Sn=An2+Bn
则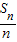
=An+B，∴{
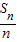}成等差数列
∵
-
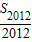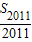=1，
∴{
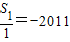
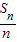}是首项为-2011，公差为1的等差数列
∴
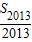=-2011+（2013-1）×1=1即S2013=2013
故选D．
点评：本题主要考查了等差数列的性质，以及构造法的应用，同时考查了转化的思想，属于基础题．
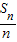=An+B，可知{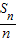}成等差数列，然后求出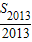的值，从而可求出所求．解答：解：设等差数列前n项和为Sn=An2+Bn
则
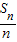=An+B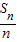，∴{}成等差数列∵
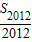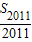-=1，∴{
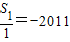
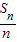}是首项为-2011，公差为1的等差数列∴
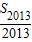=-2011+（2013-1）×1=1即S2013=2013故选D．
点评：本题主要考查了等差数列的性质，以及构造法的应用，同时考查了转化的思想，属于基础题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目