题目内容
7.已知数列{an}满足a1=1,且点(an,an+1)(n∈N*)在直线y=x+1上;数列{bn}的前n项和Sn=3n-1.(1)求数列{an},{bn}的通项公式;
(2)若数列{an•bn}的前n项和为Tn,求使Tn<8Sn+$\frac{17}{2}$成立的最大数n的值.
分析 (1)由题意可得an+1=an+1,运用等差数列的通项公式可得an=n;再由b1=S1=2;bn=Sn-Sn-1,计算即可得到所求通项;
(2)求得an•bn=2n•3n-1,运用数列的求和方法:错位相减法,结合等比数列的求和公式,可得Tn,由题意化简可得2n-1<16,解不等式即可得到所求最大值.
解答 解:(1)由题意可得an+1=an+1,
可得an=a1+n-1=1+n-1=n;
由数列{bn}的前n项和Sn=3n-1,
可得b1=S1=2;
bn=Sn-Sn-1=3n-1-(3n-1-1)=2•3n-1,
上式对n=1也成立.
则bn=2•3n-1;
(2)an•bn=2n•3n-1,
前n项和为Tn=2(1•30+2•31+3•32+…+n•3n-1),
即有3Tn=2(1•3+2•32+3•33+…+n•3n),
相减可得,-2Tn=2(1+3+32+…+3n-1-n•3n)
=2($\frac{1-{3}^{n}}{1-3}$-n•3n),
化简可得Tn=$\frac{(2n-1)•{3}^{n}+1}{2}$,
Tn<8Sn+$\frac{17}{2}$即为$\frac{(2n-1)•{3}^{n}+1}{2}$<8(3n-1)+$\frac{17}{2}$,
化简为2n-1<16,解得n<8.5,
则n的最大值为8.
点评 本题考查数列的通项的求法,注意等差数列的定义和通项公式,考查数列的求和方法:错位相减法,以及不等式恒成立问题的解法,注意运用等比数列的求和公式,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.设等差数列{an}的前n项和为Sn,若a1=-40,a6+a10=-10,则当Sn取最小值时,n的值为( )
| A. | 8或9 | B. | 9 | C. | 8 | D. | 7 |
12.若集合M={x|x>2},n={x|1<x≤3},则N∩(∁RM)等于( )
| A. | (1,2] | B. | [-2,2] | C. | (1,2) | D. | [2,3] |
19.已知函数y=xln(1+x2),则函数y的极值情况是( )
| A. | 有极小值 | B. | 有极大值 | ||
| C. | 既有极大值又有极小值 | D. | 无极值 |
17.运行下面程序,输出的结果是( )


| A. | 47 | B. | 48 | C. | 102 | D. | 123 |
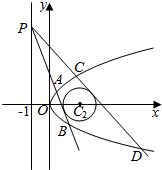 已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,
已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,