题目内容
8. 从某校高三的学生中随机抽取了100名学生,统计了某次数学模考考试成绩如表:
从某校高三的学生中随机抽取了100名学生,统计了某次数学模考考试成绩如表:| 分组 | 频数 | 频率 |
| [100,110) | 5 | 0.050 |
| [110,120) | ① | 0.200 |
| [120,130) | 35 | ② |
| [130,140) | 30 | 0.300 |
| [140,150] | 10 | 0.100 |
这些数据的频率分布直方图,再根据频率分布直方图估计这100名学生的平均成绩;
(2)从这100名学生中,采用分层抽样的方法已抽取了20名同学参加“希望杯数学竞赛”,现需要选取其中3名同学代表高三年级到外校交流,记这3名学生中“期中考试成绩低于120分”的人数为ξ,求ξ的分布列和数学期望.
分析 (1)根据频数之和为100,频率之和为1计算①②,作出频率分布直方图,利用组中值代替每小组的平均数计算平均数;
(2)根据分层原理计算选出的20名学生中成绩低于120分的人数,利用超几何分布计算概率得出分布列,再计算数学期望.
解答 解:(1)100-(5+35+30+10)=20,
1-0.05-0.2-0.3-0.1=0.35.
频率分布表为:
| 分组 | 频数 | 频率 |
| [100,110) | 5 | 0.05 |
| [110,120) | 20 | 0.2 |
| [120,130) | 35 | 0.35 |
| [130,140) | 30 | 0.3 |
| [140,150] | 10 | 0.1 |
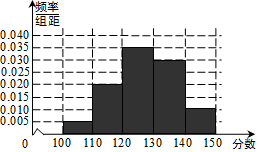
平均成绩为105×0.05+115×0.2+125×0.35+135×0.3+145×0.1=127分.
(2)成绩低于120分的人数为20×(0.05+0.2)=5人,不低于120分的人数为15人,
∴ξ的所有可能取值为0,1,2,3,
且P(ξ=0)=$\frac{{C}_{15}^{3}}{{C}_{20}^{3}}$=$\frac{91}{228}$,P(ξ=1)=$\frac{{C}_{5}^{1}{C}_{15}^{2}}{{C}_{20}^{3}}$=$\frac{35}{76}$,
P(ξ=2)=$\frac{{C}_{5}^{2}{C}_{15}^{1}}{{C}_{20}^{3}}$=$\frac{5}{38}$,P(ξ=3)=$\frac{{C}_{5}^{3}}{{C}_{20}^{3}}$=$\frac{1}{114}$.
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{91}{228}$ | $\frac{35}{76}$ | $\frac{5}{38}$ | $\frac{1}{114}$ |
点评 本题考查了频率分布直方图,离散型随机变量的分布列与数学期望,属于中档题.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角,则$2kπ-\frac{π}{2}<α<2kπ(k∈z)$ |
16.若复数z满足$\frac{z+2i}{z}$=2+3i,其中i是虚数单位,则$\overline z$=( )
| A. | $\frac{2}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{2}{5}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{3}{5}$-$\frac{1}{5}$i |
3.微信是腾讯公司推出的一种手机通讯软件,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户为“A组”,否则为“B组”,调查结果如下:
(Ⅰ)根据以上数据,能否有60%的把握认为“A组”用户与“性别”有关?
(Ⅱ)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;
(Ⅲ)从(Ⅱ)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,求“这3人中既有A组又有B组”的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| A组 | B组 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(Ⅱ)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“A组”和“B组”的人数;
(Ⅲ)从(Ⅱ)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,求“这3人中既有A组又有B组”的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| $\overrightarrow{OA}•\overrightarrow{OB}=0$ | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
20.要得到函数y=sin(2x-$\frac{π}{4}$)的图象,只要将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{4}$ | B. | 向右平移$\frac{π}{4}$ | C. | 向左平移$\frac{π}{8}$ | D. | 向右平移$\frac{π}{8}$ |
18.已知向量$\overrightarrow{a}$=(cos5°,sin5°),$\vec b=({cos65°,sin65°})$,则$|{\vec a+2\vec b}|$=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |