题目内容

如图，A是单位圆与x轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），平行四边形OAQP的面积为S（θ），
（Ⅰ）求+S（θ）的最大值及此时θ的值θ0；
（Ⅱ）设点B的坐标为，∠AOB=α，在（Ⅰ）的条件下，求cos（α+θ0）。
解：（Ⅰ）由已知，A，P的坐标分别为（1，0），（cosθ，sinθ），
∴=（1+cosθ，sinθ），=1+cosθ，
又S（θ）= sinθ，
∴+S（θ）=sinθ+cosθ+1，
故+S（θ）的最大值是，此时；
（Ⅱ），
∴。
练习册系列答案
相关题目
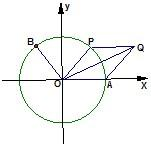精英家教网如图，A是单位圆与x轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（1）求
OA
•
OQ
+S的最大值及此时θ的值θ0；
（2）设点B的坐标为(-
3
5
，
4
5
)，∠AOB=α，在（1）的条件下求cos（α+θ0）．
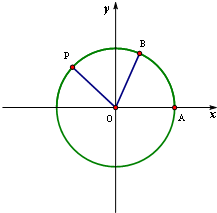如图，A是单位圆与x轴正半轴的交点，B，P为单位圆上不同的点，∠AOB=θ，∠AOP=2θ，0≤θ≤π．
（Ⅰ）当θ为何值时，
AB
∥
OP
？
（Ⅱ）若
OQ
=
OA
+
OB
，则当θ为何值时，点Q在单位圆上？
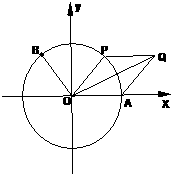（2011•普宁市模拟）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（Ⅰ）求cosα+sinα；
（Ⅱ）求
OA
•
OQ
+S的最大值及此时θ的值θ0．
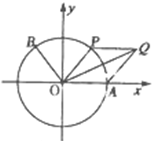（2012•茂名二模）如图，A是单位圆与x轴正半轴的交点，点B，P在单位圆上，且B（-
3
5
，
4
，5
），∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
．设四边形OAQP的面积为S，
（1）求cos（α-
π
6
）；
（2）求f（θ）=
OA
•
OQ
+S的单调递增区间．
（2012•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α．
（Ⅰ）求
4cosα-2sinα
5cosα+3sinα
的值；
（Ⅱ）令∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S，f(θ)=(
OA
•
OQ
-1)S+S2，求f（θ）的最大值及此时θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网