题目内容

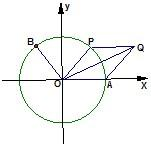精英家教网如图，A是单位圆与x轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（1）求
OA
•
OQ
+S的最大值及此时θ的值θ0；
（2）设点B的坐标为(-
3
5
，
4
5
)，∠AOB=α，在（1）的条件下求cos（α+θ0）．
分析：（1）由已知我们可得：
OA
•
OQ
+S=(
OA
)2+
OA
•
OP
+S=1+cosθ+sinθ，转化为正弦型函数，结合（0＜θ＜π），易给出
OA
•
OQ
+S的最大值及此时θ的值θ0；
（2）由已知cosα=-
3
5
，sinα=
4
5
，根据（1）的结论θ0=
π
4
，代入两角和的余弦函数公式，即可得到结论．
解答：解：（1）
OA
•
OQ
+S=
2
sin(θ+
π
4
)+1(0＜θ＜π)，
故
OA
•
OQ
+S的最大值是
2
+1，
此时θ0=
π
4
．
（2）cosα=-
3
5
，sinα=
4
5
，
cos（α+θ0）=cosαcosθ0-sinαsinθ0=-
7
2
10
．
点评：函数y=Asin（ωx+φ）（A＞0，ω＞0）中，最大值或最小值由A确定，由周期由ω决定，即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数，再根据最大值为|A|，最小值为-|A|，周期T=
2π
ω
进行求解．
练习册系列答案
相关题目
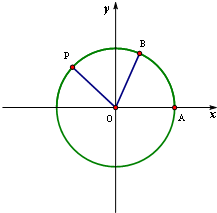如图，A是单位圆与x轴正半轴的交点，B，P为单位圆上不同的点，∠AOB=θ，∠AOP=2θ，0≤θ≤π．
（Ⅰ）当θ为何值时，
AB
∥
OP
？
（Ⅱ）若
OQ
=
OA
+
OB
，则当θ为何值时，点Q在单位圆上？
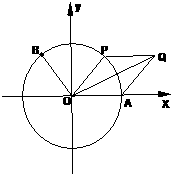（2011•普宁市模拟）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（Ⅰ）求cosα+sinα；
（Ⅱ）求
OA
•
OQ
+S的最大值及此时θ的值θ0．
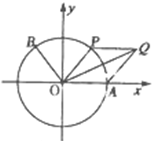（2012•茂名二模）如图，A是单位圆与x轴正半轴的交点，点B，P在单位圆上，且B（-
3
5
，
4
，5
），∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
．设四边形OAQP的面积为S，
（1）求cos（α-
π
6
）；
（2）求f（θ）=
OA
•
OQ
+S的单调递增区间．
（2012•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α．
（Ⅰ）求
4cosα-2sinα
5cosα+3sinα
的值；
（Ⅱ）令∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S，f(θ)=(
OA
•
OQ
-1)S+S2，求f（θ）的最大值及此时θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网