题目内容
8.下列命题中错误的是( )| A. | 若命题p为真命题,命题q为假命题,则命题“p∨(¬q)”为真命题 | |
| B. | 命题“若a+b≠7,则a≠2或b≠5”为真命题 | |
| C. | 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1” | |
| D. | 命题p:?x>0,sinx>2x-1,则¬p为?x>0,sinx≤2x-1 |
分析 逐项分析即可.A、根据复合命题的真值易得;B、转化为判断其逆否命题容易判断;C、否命题也要否定条件;D、由含有一个量词的命题的否定易得.
解答 解:A、若q为假,则¬q为真,故p∨(¬q)为真,故A正确;
B、命题的逆否命题为:若a=2且b=5,则a+b=7,显然正确,故原命题正确,故B正确;
C、命题“若x2-x=0,则x=0或x=1”的否命题应为“若x2-x≠0则x≠0且x≠1”,故C错误;
D、根据含有一个量词的命题的否定易得D正确.
综上可得:错误的为C.
故选:C.
点评 本题考查命题真假的判断.其中B项的判断是本题难点,转化为其逆否命题是关键.属于基础题.

练习册系列答案
相关题目
3.已知复数z满足2z+$\overline z$=6-4i(i是虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知定义在R上的函数y=f(x)满足:函数y=f(x-1)的图象关于直线x=1对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立(f′(x)是函数f(x)的导函数),若a=(sin$\frac{1}{2}$)f(sin$\frac{1}{2}$),b=(ln2)f(ln2),c=2f(log${\;}_{\frac{1}{2}}$$\frac{1}{4}$),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
18.在矩形ABCD中,点E为CD的中点,$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=$\overrightarrow b$,则$\overrightarrow{BE}$=( )
| A. | $-\frac{1}{2}\overrightarrow a-\overrightarrow b$ | B. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ | C. | $-\frac{1}{2}\overrightarrow a+\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a+\overrightarrow b$ |
 如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.
如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.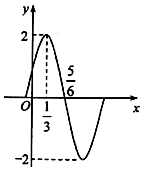 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的图象(部分)如图.
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的图象(部分)如图.