题目内容
15.已知O为坐标原点,过双曲线${x^2}-\frac{y^2}{a^2}=1$上的点P(1,0)作两条渐近线的平行线,交两渐近线分别于A,B两点,若平行四边形OBPA的面积为1,则双曲线的离心率为$\sqrt{5}$.分析 作出对应的图象,求出交点坐标,结合平行四边形的面积建立方程关系求出a的值进行求解即可.
解答 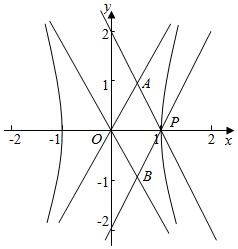 解:双曲线的渐近线方程为y=±ax,(不妨设a>0),
解:双曲线的渐近线方程为y=±ax,(不妨设a>0),
设与y=-ax平行且过P的直线方程为y=-a(x-1)=-ax+a,
由$\left\{\begin{array}{l}{y=ax}\\{y=-ax+a}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{1}{2}a}\end{array}\right.$,即A($\frac{1}{2}$,$\frac{1}{2}$a)
则平行四边形OBPA的面积S=2S△OBP=2×$\frac{1}{2}$×1×$\frac{1}{2}$a=$\frac{1}{2}$a=1,得a=2,
即双曲线的方程为x2-$\frac{{y}^{2}}{4}$=1,
则双曲线的a1=1,b1=2,
则c=$\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}}$=$\sqrt{5}$,
即双曲线的离心率e=$\frac{c}{{a}_{1}}$=$\frac{\sqrt{5}}{1}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$
点评 本题主要考查双曲线离心率的求解,根据条件求出交点坐标,结合平行四边形的面积进行求解是解决本题的关键.

练习册系列答案
相关题目
6.双曲线$\frac{{x}^{2}}{3}$-y2=1的焦点F到其渐近线的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
10.已知双曲线C:$\frac{x^2}{16}-\frac{y^2}{b^2}=1({b>0})$的右焦点与抛物线y2=20x的焦点重合,则双曲线C的渐近线方程为( )
| A. | 4x±3y=0 | B. | 3x±4y=0 | C. | 16x±9y=0 | D. | 9x±16y=0 |
4.设抛物线x2=2py(8≥p>0)的焦点为F,点A、B为抛物线上两个动点,过弦AB的中点M作抛物线的准线的垂线MN,垂足为N,当|AF|•|BF|=16时,|MN|的最小值为( )
| A. | 6 | B. | 4 | C. | 8 | D. | 16 |
5.计算机执行下面的程序段后,输出的结果是( )
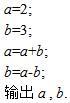
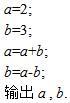
| A. | 5,2 | B. | -1,5 | C. | 5,-1 | D. | 2,5 |
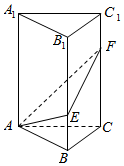 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.