题目内容
已知函数f(x)=2sin(π-x)•cosx+sin2x-cos2x,x∈R.
(Ⅰ)求f(
)的值及函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在[0,π]上的单调减区间.
(Ⅰ)求f(
| π |
| 2 |
(Ⅱ)求函数f(x)在[0,π]上的单调减区间.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用诱导公式以及二倍角公式化简函数的表达式为一个角的一个三角函数的形式,
(Ⅰ)直接求f(
)的值,直接求出函数f(x)的最小正周期;
(Ⅱ)利用函数的单调减区间求解函数f(x)在[0,π]上的单调减区间.
(Ⅰ)直接求f(
| π |
| 2 |
(Ⅱ)利用函数的单调减区间求解函数f(x)在[0,π]上的单调减区间.
解答:
解:∵f(x)=2sin(π-x)•cosx+sin2x-cos2x=sin2x-cos2x=
sin(2x-
).
(Ⅰ)f(
)
sin(2×
-
)=
×
=1.
显然,函数f(x)=
sin(2x-
).
的最小正周期为π.…(8分)
(Ⅱ)令2kπ+
≤2x-
≤2kπ+
得
kπ+
≤x≤kπ+
,k∈Z.
又x∈[0,π],∴x∈[
,
].
函数f(x)在[0,π]上的单调减区间[
,
]. …(13分)
| 2 |
| π |
| 4 |
(Ⅰ)f(
| π |
| 2 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
显然,函数f(x)=
| 2 |
| π |
| 4 |
的最小正周期为π.…(8分)
(Ⅱ)令2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
kπ+
| 3π |
| 8 |
| 7π |
| 8 |
又x∈[0,π],∴x∈[
| 3π |
| 8 |
| 7π |
| 8 |
函数f(x)在[0,π]上的单调减区间[
| 3π |
| 8 |
| 7π |
| 8 |
点评:本题考查三角函数的化简求值,考查三角函数的基本性质的应用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知不等式
>0的解集为(-1,2),则二项式(ax-
)6展开式的常数项是( )
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、-15 | B、15 | C、-5 | D、5 |
设复数z满足(z+1)i=-3+2i(i为虚数单位),则z的实部是( )
| A、1 | B、2 | C、3 | D、4 |
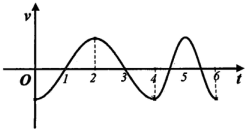
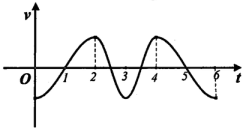
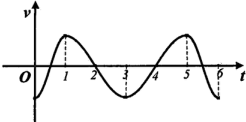
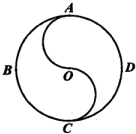 如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )
如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )