题目内容
10.已知a、b、c是直线,α是平面,给出下列命题:①若a∥b,b⊥c,则a⊥c;
②若a⊥b,b⊥c,则a∥c;
③若a∥α,b?α,则a∥b;
④若a⊥α,b?α,则a⊥b;
⑤若a与b异面,则至多有一条直线与a、b都垂直.
⑥若a?α,b?α,a⊥c,b⊥c,则a∥b.
其中真命题是①④.(把符合条件的序号都填上)
分析 利用空间线线关系和线面关系定理进行判断选择.
解答 解:①若a∥b,b⊥c,则a⊥c;①正确
②若a⊥b,b⊥c,则a∥c相交或者异面;②错误
③若a∥α,b?α,则a∥b或者异面; ③错误;
④若a⊥α,b?α,由线面垂直的下性质定理得到a⊥b;④正确;
⑤若a与b异面,则有无数条直线与a、b都垂直.⑤错误;
⑥若a?α,b?α,a⊥c,b⊥c,则a∥b或者相交;故⑥错误;
故答案为:①④
点评 本题考查了空间直线位置关系的判断;考查空间想象能力;熟练掌握相关的定理是解答的关键.

练习册系列答案
相关题目
20.设tanα,tanβ是方程x2+3x-2=0的两个根,则tan(α+β)的值为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
1.已知集合A={x|0<x<2},B={x|1-x2>0},则A∩(∁RB)=( )
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
5.为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如表:
(Ⅰ)求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
19.如图中的网格纸是边长为1的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为( )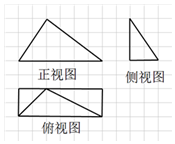

| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
