题目内容
14.过点P(4,8)且被圆x2+y2=25截得的弦长为6的直线方程是( )| A. | 3x-4y+20=0 | B. | 3x-4y+20=0或x=4 | C. | 4x-3y+8=0 | D. | 4x-3y+8=0或x=4 |
分析 由圆的方程,可知圆心(0,0),r=5,圆心到弦的距离为4,若直线斜率不存在,则垂直x轴x=4,成立;若斜率存在,由圆心到直线距离d=$\frac{|-4k+8|}{\sqrt{{k}^{2}+1}}$=4,即可求得直线斜率,求得直线方程.
解答 解:圆心(0,0),r=5,圆心到弦的距离为4,
若直线斜率不存在,则垂直x轴
x=4,圆心到直线距离=|0-4|=4,成立;
若斜率存在
y-8=k(x-4)即:kx-y-4k+8=0
则圆心到直线距离d=$\frac{|-4k+8|}{\sqrt{{k}^{2}+1}}$=4,解得k=$\frac{3}{4}$,
综上:x=4和3x-4y+20=0,
故选B.
点评 本题主要考查直线与圆的位置关系,主要涉及了圆心距,弦半距及半径构成的直角三角形,直线的方程形式及其性质,属于中档题.

练习册系列答案
相关题目
19.若存在两个正实数x,y,使得等式2x+a(y-2ex)(lny-lnx)=0成立,则实数a的取值范围为( )
| A. | $[{-\frac{1}{2},\frac{1}{e}}]$ | B. | $({0,\frac{2}{e}}]$ | C. | $({-∞,0})∪[{\frac{2}{e},+∞})$ | D. | $({-∞,-\frac{1}{2}})∪[{\frac{1}{e},+∞})$ |
4.数列{an}满足:a1=3,an+1=an-2,则a100等于( )
| A. | 98 | B. | -195 | C. | -201 | D. | -198 |
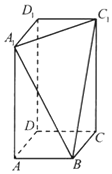 长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$
长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$ 已知函数y=|x|(x-4)
已知函数y=|x|(x-4)