题目内容
3. 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.(1)求函数的解析式;
(2)设0<x<π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围.
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)由题意可得在(0,π)上,函数$f(x)=2sin(2x+\frac{π}{6})$和y=m(m∈R)的图象有2个不同的交点,数形结合可得m的范围.
解答  解:(1)观察图象,得$A=2,T=(\frac{11π}{12}-\frac{π}{6})×\frac{4}{3}=π$.∴$ω=\frac{2π}{T}=2$,∴f(x)=2sin(2x+φ),
解:(1)观察图象,得$A=2,T=(\frac{11π}{12}-\frac{π}{6})×\frac{4}{3}=π$.∴$ω=\frac{2π}{T}=2$,∴f(x)=2sin(2x+φ),
∵函数经过点$(\frac{π}{6},2)$,∴$2sin(2×\frac{π}{6}+φ)=2$,即$sin(\frac{π}{3}+φ)=1$,又∵$|φ|<\frac{π}{2}$,∴$φ=\frac{π}{6}$.
∴函数的解析式为$f(x)=2sin(2x+\frac{π}{6})$.
(2)∵0<x<π,∴f(x)=m的根的情况,相当于$f(x)=2sin(2x+\frac{π}{6})$与g(x)=m的交点个数情况,且0<x<π,
∴在同一坐标系中画出$f(x)=2sin(2x+\frac{π}{6})$和y=m(m∈R)的图象.
由图象可知,当-2<m<1或1<m<2时,直线y=m(m∈R)与曲线有两个不同的交点,
即原方程有两个不同的实数根,∴m的取值范围为-2<m<1或1<m<2.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值.方程根的存在性以及个数的判断,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
11.某地最近十年粮食需求量逐年上升,如表是部分统计数据:
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程y=bx+a;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
提示:线性回归方程y=a+bx,$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$.
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
提示:线性回归方程y=a+bx,$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$.
12.下列说法中,正确的是( )
| A. | 幂函数的图象都经过点(1,1)和点(0,0) | |
| B. | 当α=0时,函数y=xα的图象是一条直线 | |
| C. | 若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大 | |
| D. | 幂函数y=xα,当α<0时,在第一象限内函数值随x值的增大而减小 |
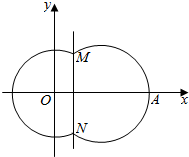 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0). 某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.